Let success metric(for some business use case I am working on) be a continuous random variable S. The mean of pdf defined on S indicates the chance of success. Higher the mean more is the chance of success. Let std dev of pdf defined on S indicates risk. Lower the std deviation lower the risk of failure.
I have data,let's call them X, which affects S. Let X also be modelled as bunch of random variables.
P(S|X) changes based on X. The problem statement is I want to pick Xs such that P(S|X) has mean higher than P(S) and std deviation lower than P(S).
Just to illustrate my point I have taken X of 1 dimension. Scatter plot between X(horizontal) and Y(on vertical):
You can see that P(S|X) changes for different values of X as given in the below plot:
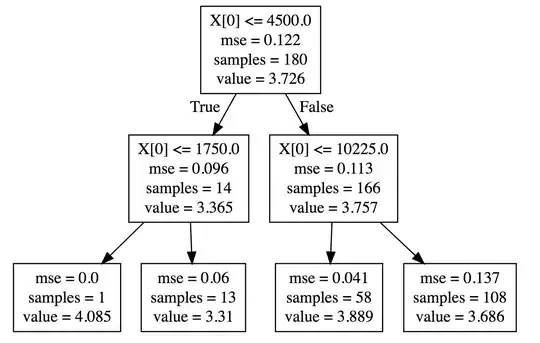
For X between 4500 and 10225, mean of S is 3.889 and std dev is 0.041 compared to mean of 3.7 and std dev of 0.112 when there is no constraint on X.
What I am interested in is given S and bunch of Xs... pick range of Xs such that resulting distribution of P(S|X) has higher mean and lower standard deviation... Please help me find a standard technique that would help me achieve this.
Also I don't want to condition on X such that number of samples are too small to generalise.I want to avoid cases such as on the left most side of tree where number of samples is 1.
