Pattern Recognition, Bishop - (Linear) Discriminant Functions 4.1

Question

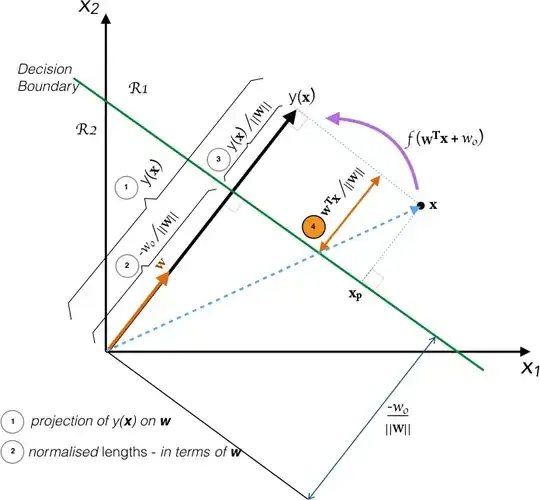
Please refer "Pattern Recognition and Machine Learning" - Bishop, page 182.

I am struggling to visualize the intuition behind equations 4.6 & 4.7. I am presenting my understanding of section 4.1.1 using the diagram:

---

Pls. Note: I have used $x_{\perp}$ and $x_{p}$ interchangeably.

Equations 4.6, 4.7 from book: $$\mathbf{x} = \mathbf{x_{\perp}} + \textit{r}\mathbf{\frac{w}{\Vert{w}\Vert}} \tag {4.6}$$ Muiltiplying both sides of this result by $\mathbf{w^{T}}$ and adding $w_{0}$, and making use of $y(\mathbf{x}) = \mathbf{w^{T}x} + w_{0}$ and $y(\mathbf{x_{\perp}}) = \mathbf{w^{T}x_{\perp}} + w_{0} = 0$, we have $$r = \frac{y(\mathbf{x})}{\Vert{\mathbf{w}}\Vert} \tag{4.7}$$

Questions:

1. Is $y(\mathbf{x})$ the (orthogonal) projection of $(\mathbf{w^{T}x} + w_{0})$ along $\mathbf{w}$, the weight vector?
2. Are the lengths normalized to express them as multiples of unit vector $\mathbf{\frac{{w}}{\Vert{w}\Vert}}$. If so, can the distance $r = $$\frac{y(\mathbf{x})}{\Vert\mathbf{w}\Vert}$ exceed 1.
3. Given that, $$ y(\mathbf{x}) = \mathbf{w^{T}x} + w_{0}$$ i.e. $y(\cdot)$ has two parts: $\textit{orthogonal component above/ below}$ decision boundary, and the $\textit{bias}$. And so, I'm calculating $y(\cdot)$ as:

$$y(\mathbf{x}) = \mathbf{\frac{w^{T}x}{\Vert{w}\Vert}} + \frac{w_{0}}{\Vert\mathbf{w}\Vert}$$ while the book gets it as: $$y(\mathbf{x}) = {\frac{y(\mathbf{x})}{\Vert\mathbf{w}\Vert}} + \frac{w_{0}}{\Vert\mathbf{w}\Vert}$$ I am struggling to visualize how do we get the first term in the equation above (in book, eqn. 4.7)

Alternatively, presenting my doubt/argument w.r.t. to book eqns 4.6 & 4.7; by substituting $r$ (eq. 4.7) into eq. 4.6 we get: $$\mathbf{x} = \mathbf{x_{p}} + y(\mathbf{x}) \qquad {(\Vert{\mathbf{w}}\Vert^{2} = \mathbf{w})}$$

which again seems to be incorrect - by triangle rule of vector addition.

Given the context, where am I losing track? Request your inputs.

Answer 1

1. No, $y(\mathbf{x})=\mathbf{w}^T\mathbf{x}+w_0$; it is a scalar. The dot product $\mathbf{w}^T\mathbf{x}$ is $\|\mathbf{w}\|$ times the length of the projection of $\mathbf{x}$ onto $\mathbf{w}$. $w_0$ in your figure would be negative, and has the property that $y(\mathbf{x})=0$ whenever $\mathbf{x}$ is on the decision boundary.

2. No normalization appears to be necessary. Certainly $r$ can be arbitrarily large (either positive or negative), when $\mathbf{x}$ is far away from the decision boundary.

3. As mentioned previously, the first term is actually a length from the origin; the bias serves to shift this so that $y$ itself is the orthogonal (scalar) component [up to scaling by $\|w\|$...But that's what we're out to show when we pass from Eq(4.6) to (4.7)].

The text's approach is to decompose $\mathbf{x}$ into components relative to the decision boundary: $\mathbf{x}_{\perp}$ on the boundary, and something perpendicular to the boundary. Being perpendicular to the boundary, it is in the direction of $\mathbf{w}$, but we don't know how far, so they introduce its length as the unknown $r$. (There's some standard geometry stuff here that could also get us to the conclusion, but I'll explain their approach.)

Now, as mentioned before, $y$ is zero on the boundary, so they have $y(\mathbf{x}_{\perp})=0$. And now, just to fill in some of the details of what they say, $$\begin{align*} \mathbf{x} &= \mathbf{x}_{\perp} + r \frac{\mathbf{w}}{\|\mathbf{w}\|}\\ \mathbf{w}^T\mathbf{x}+w_0 &= \mathbf{w}^T\mathbf{x}_{\perp}+w_0 + r \frac{ \mathbf{w}^T\mathbf{w} }{ \|\mathbf{w}\| } \\ y(\mathbf{x}) &= y(\mathbf{x}_{\perp}) + r \frac{\|\mathbf{w}\|^2}{\|\mathbf{w}\|} \\ y(\mathbf{x}) &= 0 + r \|\mathbf{w}\|, \end{align*}$$ and so $r=y(\mathbf{x})/\|\mathbf{w}\|$ as desired.

[I'm not sure what you meant in your last few lines; at least some of it seems to have been a typo? Feel free to follow up.]

---

EDIT: Regarding your addition about substituting $r$, you should get $$\mathbf{x}=\mathbf{x}_{\perp}+y(\mathbf{x})\frac{\mathbf{w}}{\|\mathbf{w}\|^2},$$ but $\|\mathbf{w}\|^2$ is not equal to $\mathbf{w}$; the former is a scalar, and the latter a vector! Rewriting, we have $$\mathbf{x}=\mathbf{x}_{\perp}+\frac{y(\mathbf{x})}{\|\mathbf{w}\|}\frac{\mathbf{w}}{\|\mathbf{w}\|}.$$ This now looks correct: from the origin, go to $\mathbf{x}_{\perp}$, then along the unit vector $\mathbf{w}/\|\mathbf{w}\|$ for a distance of $y(\mathbf{x})/\|\mathbf{w}\|$ (which, per your bubble3, is the correct distance).