9

A website (on page 4) says:

The correlation coefficient is a measure of linear relationship and thus a value of r = 0 does not imply there is no relationship between the variables. For example in the following scatterplot which implies no (linear) correlation however there is a perfect quadratic relationship.

What is the meaning of a perfect quadratic relationship?

Glorfindel
  • 289
  • 1
  • 6
  • 13
Subhash C. Davar
  • 578
  • 4
  • 18
  • I just wanna mention if the distribution is gaussian, that, $r=0$, does imply independence. – Green Falcon Apr 23 '20 at 04:03
  • 1
    What @Media means is when the **joint** distribution is Gaussian. Uncorrelated univariate Gaussians can be dependent; they just won’t be jointly Gaussian. – Dave Apr 23 '20 at 04:11
  • 1
    There also is a good description on Wikipedia: https://en.wikipedia.org/wiki/Pearson_correlation_coefficient – Peter Apr 23 '20 at 10:34

2 Answers2

7

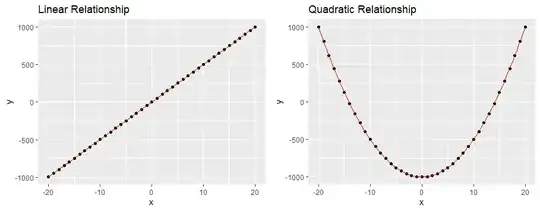
Below I have graphed a linear and quadratic function, $y = 50x + 3$ and $y=5x^2 - 1000$, respectively.

Before calculating anything, we can observe that $x$ and $y$ are related to one another in some form. If we describe in words, we can say for the left plot that as $x$ increases so does $y$.

Similarly, for the right plot, we can say that as $x$ moves towards 0, from the left, $y$ decreases towards 0, and as $x$ moves away from 0 towards the right, $y$ increases.

In fact, $x$ and $y$ have a perfect linear relationship in the left plot, while $x$ and $y$ has a perfect quadratic relationship in the right plot. We can say this because the points, in both plots, lie on the red line

enter image description here

If we take it a step further and calculate the correlation between x and y.

We observe for the linear relationship that $x$ and $y$ has a correlation of 1. In contrast, for the quadratic relation, $x$ and $y$ has a correlation of 0.

Below you will find R code for the plot above, in addition, code to calculate the correlation coefficients

set.seed(1)
library(ggplot2)
library(dplyr)
library(gridExtra)

# Linear Function
linear = function(x){(50)*x + 3 }

# Quadratic Function
quadratic = function(x){(5)*x^2 - 1000}

# Create Data Frame
df = data.frame(x = c(-20:20), 
                y = c(sapply(-20:20, quadratic),sapply(-20:20, linear)), 
                type = c(rep('quadratic',41),rep('linear',41)) )

# Plot Functions
lp = ggplot(subset(df,type == 'linear'), aes(x,y)) + geom_point() + 
  stat_function(fun=linear, colour="red") + ggtitle('Linear Relationship')

qp = ggplot(subset(df,type == 'quadratic'), aes(x,y)) + geom_point() + 
  stat_function(fun=quadratic, colour="red") + ggtitle('Quadratic Relationship')

grid.arrange(lp, qp, ncol=2)


# Calculate correlation coefficients
df %>% filter(type =='linear') %>% select(x,y) %>% cor %>% (function(x){x[1,2]})
df %>% filter(type =='quadratic') %>% select(x,y) %>% cor %>% (function(x){x[1,2]})
nwaldo
  • 371
  • 2
  • 10
5

The perfect quadratic relationship means that the point lie perfectly on some parabola.

Consider a perfect linear relationship: points lying in a straight line, such as $(1,2)$, $(2,5)$, and $(5, 14)$ that are on $y=3x-1$.

Ditto for points lying perfectly on some parabola giving a perfect quadratic relationship. Consider $(-2,4)$, $(1,1)$, $(0,0)$, $(1,1)$, and $(2,4)$ that lie on $y=x^2$.

Dave
  • 3,841
  • 1
  • 8
  • 23