In this paper they have this equation, where they use the score function estimator, to estimate the gradient of an expectation. How did they derive this?
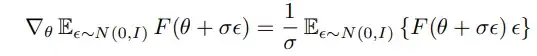
- 203
- 1
- 2
- 7
- 13
- 2
1 Answers
This is simply a special case (where $p_\psi = N(0,1)$) of the general gradient estimator for Natural Evolution Strategies (proved in another reference, look it up):
Outline of derivation based on the general formula for the gradient estimator:
$$\nabla_\psi E_{\theta \sim p_\psi} \left[ F(\theta) \right] = E_{\theta \sim p_\psi} \left[ F(\theta) \nabla_\psi log({p_\psi}(\theta)) \right]$$
If
$$\epsilon \sim \mathbb{N}(0, 1) = \frac{1}{\sqrt{2 \pi}}e^{-\frac{\epsilon^2}{2}}$$
$$\psi = \theta + \sigma \epsilon \sim \mathbb{N}(\theta, \sigma) = \frac{1}{\sigma\sqrt{2 \pi}}e^{-\frac{(\psi-\theta)^2}{2\sigma^2}}$$
Thus: $\psi = \theta + \sigma \epsilon \sim \mathbb{N}(\theta, \sigma) \Longleftrightarrow \epsilon = \frac{\psi-\theta}{\sigma} \sim \mathbb{N}(0,1)$
So:
$$\begin{align} \nabla_\theta E_{\psi \sim N(\theta,\sigma)} \left[ F(\theta + \sigma \epsilon) \right] &= E_{\psi \sim N(\theta,\sigma)} \left[ F(\theta + \sigma \epsilon) \nabla_\theta (-\frac{(\psi-\theta)^2}{2\sigma^2}) \right] \\ &= E_{\epsilon \sim N(0,1)} \left[ F(\theta + \sigma \epsilon) \nabla_\epsilon (-\frac{\epsilon^2}{2}) \frac{d(\frac{\psi-\theta}{\sigma})}{d\theta} \right] \\ &= \frac{1}{\sigma} E_{\epsilon \sim N(0,1)} \left[ F(\theta + \sigma \epsilon) \epsilon \right] \\ &= \nabla_\theta E_{\epsilon \sim N(0,1)} \left[ F(\theta + \sigma \epsilon) \right] \end{align}$$
note: scalar variables were considered in above steps for simplicity, but easy to extend/derive for vector variables
- 2,301
- 1
- 6
- 11
-
1I realized how to do it. There is a few steps. First substitute p with the probability density function of the normal distribution. Then the log end exp cancels out each other. Then you derive the squared term using the chain rule. Finally theta falls out. – adam Jul 26 '20 at 11:33
-
@adam, glad you figured it out! Updated answer with sample derivation steps as well – Nikos M. Jul 26 '20 at 12:57