Problem Setup: Offline contextual bandit with logs of form - <input_context, action, reward>.
Model: A logging/behavior policy $\pi_0$ is used to collect the log data, with context $x_i$, action $y_i \sim \pi_0(. \vert x_i)$, the reward from the env. $\delta(x_i, y_i)$. A new policy $\pi_{\theta}$ which needs to be learned.
Loss function: To learn the new policy $\pi_{\theta}$, the paper Variance Regularized Counterfactual Risk Minimization via Variational Divergence Minimization introduces an Importance Sampling based loss function with a constraint on the divergence b/w the new policy. 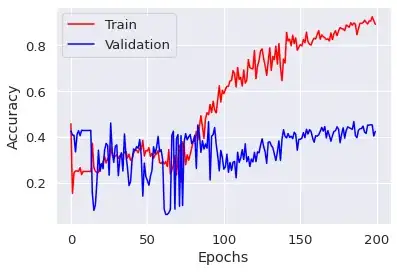
This is derived from a generalization bound 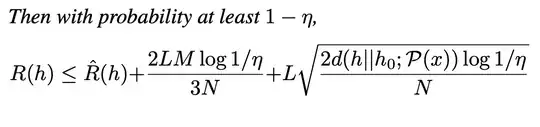 .
.
Authors argue that optimizing the bound (RHS) directly is difficult using SGD, so they propose a constraint optimization view, where at each iteration of optimization, in one step, the IPS weight risk is optimized followed by optimizing the divergence in another step.
The reasoning for alternate optimization working better than directly optimizing a linear combination of risk and divergence is not discussed in detail. Is there a theoretical reason for linear combination of different losses not working well?