TLDR: I am trying to predict the probability of an incident occurring within a specific time interval. I have data from multiple years, and I know the exact time of year that incidents occur. I have created a baseline model that takes in a time interval and returns the probability of at least one incident occurring within that interval. The model works well within a window of 7 days, but I want to be able to predict over the entire year. To do this, I am using a rolling time interval and making predictions every k days, where k is less than or equal to 7. However, I am unsure how to properly evaluate the model. I want to be able to consider both the classification error (whether the prediction was correct or not) and the time error (how close the prediction was to the actual time of the incident). I am considering using traditional regression metrics like RMSE, but I am not sure if that is appropriate since my target labels are 0s and 1s and not continuous values. I am looking for suggestions on how to evaluate and compare models in this situation.
Problem:
- I am trying to predict when in time incidents will occur
- I know the exact time in the year incidents occur
- I have time seires features too but for this question I ignore them for now, the only input is time of year
- I have multiple years of incident data (it's seasonal)
Our aim:
- Predict the probability of at least one incident occurring in a time interval.
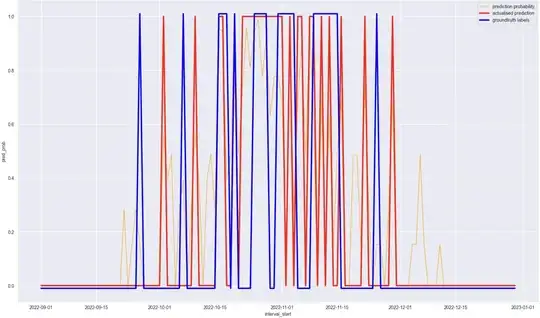
I've created a simple baseline model, the details aren't important. Given a time interval $t=(t_{start}, t_{end})$ the model returns $P(X>0)$. Using our training data, I know if an incident occurred in any time interval.
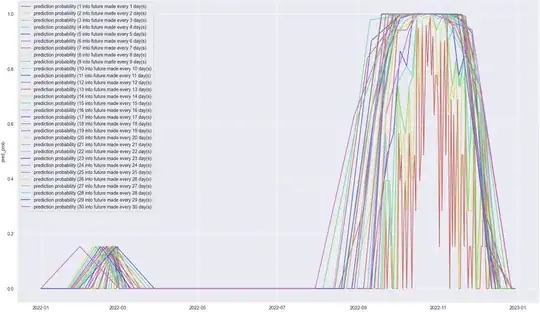
This model can only predict on a time interval of a set window (7 days) and it does a pretty good job within any given 7 day interval. To get a prediction over the whole year, I use a rolling time interval over the year and predict (prediction on 7 day interval every $k$ days, where $k\leq7$).
Again I don't think these details are important. My problem is that I don't know how to evaluate this model properly, and I've come to the conclusion that this is just a flawed approach to modelling the problem.
If I use traditional classification metrics like accuracy, precision, recall, etc. The model can not tell me if predictions were close to true labels e.g. on a 7 day interval there was indeed an incident (target label is 1), but the model predicted a probability well below 50% so the prediction is 0 but the next adjacent 7 day interval had no incident (target label is 0) but the model predicted there would be an incident (1) - now yes the model is wrong in a classification sense but it did pretty well in the time sense. It correctly identified that an incident would happen within a few days. How do I quantify both classification and the time error?
I thought about using traditional regression metrics like RMSE, but this doesn't make sense because our target label is 0s and 1s, so the 'optimal' function would be some weird square wave bouncing between 0 and 1. I'm just very confused about how to evaluate/compare two different models with an evaluation metric. I know I can maybe create my own but I don't want to do that because something seems off.