TL;DR
What is the best way to extract SPO triples from free-text with as little information loss as possible under the constraint that the nodes and relationships in the extracted triples are contained in a given ontology?
Details
I am trying to build a knowledge graph (KG) from free-text. As stated in this paper by Nickel et al. (2015), open information extraction (openIE) techniques typically lead to very sparse adjencency tensors that are often difficult to use in down-stream applications. To avoid this issue, I would like the resulting KG to feature only nodes and relationships of specific, pre-defined types as given by an ontology.
Question
Assuming, such an ontology exists, what is the best way to extract as much information from the free-text as possible and align the triples with the ontology?
For me the naive way would be to go for a two-step approach where
- I first perfom openIE and
- then I classify the extracted nodes and edges into the classes given by the types in the ontology.
I am wondering if there is a (simpler) way that does not require the detour to do openIE first.
Example: Let's start from the following free text.
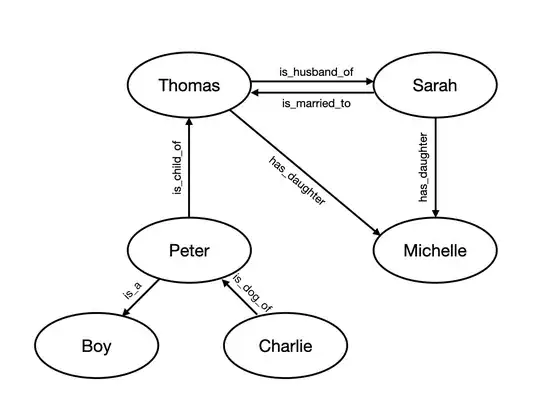
"Thomas is Sarah's husband. She married him a couple of years ago. Together they have a little daughter, Michelle. Peter, an 8-year old boy, is Thomas's second child and Charlie is Peter's dog."
Let us assume that using openIE we would be able to extract a KG like this one:
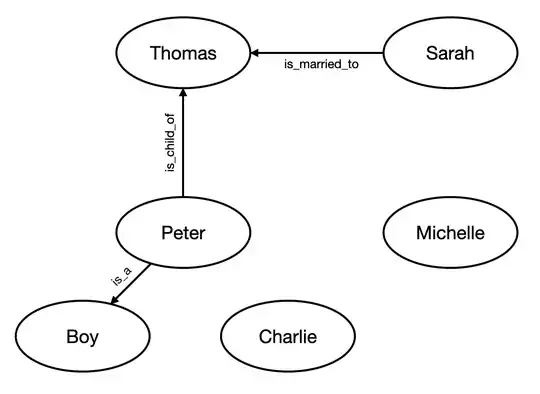
However, let's further assume that our ontology only knows the following relationships:
- is_married_to
- is_child_of
- is_pet_of
- is_a
The desired output looks therefore as follows:
NOTICE: Notice that in this example the relationships "is_husband_of" was mapped to "is_married_to" and the relationship "has_daughter" is mapped to the relationship "is_child_of" (direction is inverted). I would like to avoid loss of information as a result of retaining only those relationships that happen to be aligned with the ontology. Explicitly, the KG below would not be an acceptable solution:
Does anyone know any suitable algorithms or literature where such approaches are described?