How to make machine learning specifically for an individual in a group when we have the data on the group?

Question

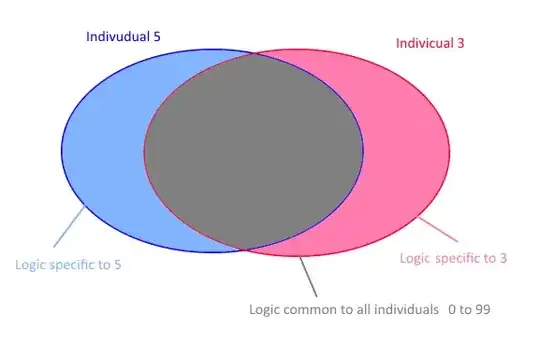
Lets specify the question with the help of the figure below: We know that one part of the behaviour (our target Y) will depend on common parameters (for the group). It is represented by the grey zone on the figure. And that one part is parameters specific to each individual. ( It is represented by the pink and blue zone )

The precise question is:

Knowing that we have data from the entire group. How to use all the data of the groups, to create a specific model for an individual of this group? The idea is to get a solid model/result because it is based on all the available data, but still specific to an individual. I imagine an answer in the form of a short list of techniques to achieve that.

Let’s illustrate the question with an example:

We do a study of 100 people. Let’s name the people [0, 1, 2, 3, 4, 5 … 99] For each person, we do a study of 30 days. Every day, we do 5 measurements of the emotion of the person (X). And then a measure of the quantify of calories in the evening meal (Y).

In this example, the goal, using machine learning, is knowing X on day 55 (after the tests), for person number 3, to be able to predict Y (on day 55) for a given person. I often came across this problem. With my experiments, tests and research, I see two possibilities:

• The first option is to take all the samples. 100 people * 30 measurements (of 5 samples x and y) = 3000 points. We create a model that connects x to y. Then we take the new x (for person number 3), and ‘predict’ y. We then have an answer that takes into account all the observations but is not the specificity of the person number 3. The model and the answer are kind of an ‘average behavioural response’ for the population. This model corresponds more to the grey zone of the figure you see above.

• The second option is to take only information from person 3 to create the model. We have 30 points. We create a model that connects x to y. The model is really specific to person 3. Since the model uses fewer points, it is less accurate. We did not use our total knowledge/data of the grey zone.

I have the deep intuition that there is a way to do better than these two options. I tried a lot but without satisfying success.

I tried, with random forest algorithms, to use all data at the same time and add an id in X vectors. This id represents the individual. It does not seem to have worked. The internet searches I have done on this topic give me unrelated results. Any help or keywords on this topic are welcome.

Is it useful or necessary that I share an example dataset?

Answer 1

There are a number of other options. The way to select between them is to ask yourself: How are you going to deploy this classifier? What data will be available to the classifier?

It's possible to build a single model that still has the ability to personalize for a particular person. You do that by adding another attribute that identifies the person; typically, this would be encoded as a one-hot vector, so you have 3000 data points, and each data point has some features realted to their emotion measurement(s), plus 100 more features for the one-hot-encoded identity vector.

The exact details depend on what data will be available at test time. Suppose that you will try to predict the number of calories in the evening meal based on the emotion measurements over the past week. Then you have $100 \times (30-6) = 2400$ data points (the first 6 days from each person aren't usable because you don't have a week of emotion measurements yet). Each data point has 135 features: 35 features for the emotion measurements over the past 7 days, and 100 features for the one-hot-encoded vector. Then you train a model on this.

If you use this kind of approach, you need to be careful about how you split the data into training, validation, and test sets. I suggest you split by person not by data point; so if you want a 60/20/20 split, you pick 60 people to be in the training set (leading to $60 \times 24$ data points in the training set, 20 people to be in the validation set ($20 \times 24$ data points), and 20 people for the test set ($20 \times 24$ data points). This is based on a deployment scenario where you train a single model once based on some people's data, and then to predict calories for a new person, you don't retrain it based on historical data from the new person.

Hopefully you can see how to adjust this based on the deployment scenario. The basic principle is to figure out how the classifier will be used in practice, and then choose an evaluation strategy that matches how it will be used.

---

Another option is to first try to cluster the users into a few clusters, and build a classifier to predict which cluster each person is in. Then, build one model per cluster.

---

A third option is to try to identify some additional attribute of the person that will help you predict their calory consumption. Add this as an additional feature (W). For instance, this might be gender or demographics or anything else that you think has predictive power.