Bishop's Perceptron loss
On one hand, it is stated in equation 4.54 of Chris Bishop's book (pattern recognition and machine learning) that the loss function of perceptron algorithm is given by:
$${E_p}(\mathbf{w}) = - \sum\limits_{n \in M} {{\mathbf{w}^T}{\phi _n}} {t_n}$$
where $M$ denotes the set of all misclassified data points.
Original Perceptron loss
On the other hand, The loss function used in the original perceptron paper written by Frank Rosenblatt is given by (wikipedia):
$${1 \over s}\sum\limits_{j = 1}^s {\left| {{d_j} - {y_j}\left( t \right)} \right|} $$ which when translated to the notation of Bishop's book is given by:
$${1 \over N}\sum\limits_{n = 1}^N {\left| {{t_n} - {\mathbf{w}^T}{\phi _n}} \right|} $$ where $N$ denotes the set of all data points.
My question
My question is that why Bishop's version of Perceptron loss is different from the original paper? Considering Bishop's book as a highly recognized book in machine learning field, can we call it Bishop's Perceptron?!
Scikit-learn's implementation
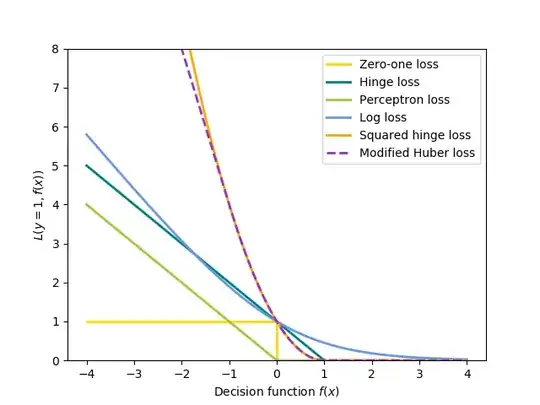
By the way, it seems that Scikit-learn uses Bishop's version of Perceptron loss (Scikit-learn documentation). It is apparent from the following formula and figure:
-np.minimum(xx, 0)
which for one sample reduces to: $$ - \min \left( {0,{\mathbf{w}^T}{\phi _n}{t_n}} \right)$$