Combining Latitude/Longitude position into single feature

Question

I have been playing with two dimensional machine learning using pandas (trying to do something like this), and I would like to combine Lat/Long into a single numerical feature -- ideally in a linear fashion. Is there a "best practice" to do this?

Answer 1

A note: for those who've ended here looking for a hashing technique, geohash is likely your best choice.

Representing latitude and longitude in a single linear scale is not possible due to the fact that their domain is inherently a 3D space. Reducing that as per your needs would require a spatial flattening technique that's unheard of to me.

Reasoning

As far as lat/long merging goes, the best of best practices would be to resort to the Haversine formula, which calculates the distance between two points over a spherical surface, and receives those points' coordinates as input.

One way to incorporate that in your use case - where each point should probably have an independent lat/long combination - would be to assume the distance's origin point coordinates to be $(\varphi_1, \lambda_1) = (0, 0)$, which would render

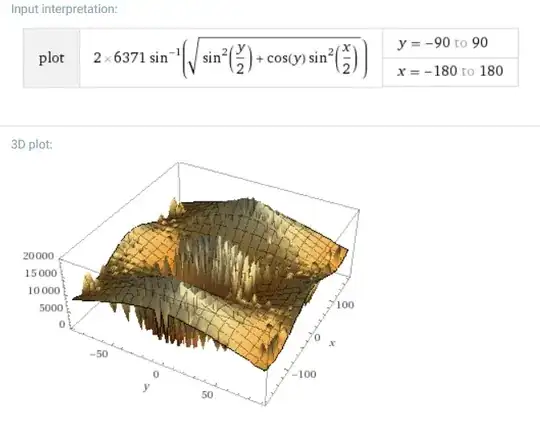
$$d =2r \arcsin\left(\sqrt{\sin^2\left(\frac{\varphi_2 - 0}{2}\right) + \cos(0) \cos(\varphi_2)\sin^2\left(\frac{\lambda_2 - 0}{2}\right)}\right)$$

$$= 2r \arcsin\left(\sqrt{\sin^2\left(\frac{\varphi_2}{2}\right) + \cos(\varphi_2)\sin^2\left(\frac{\lambda_2}{2}\right)}\right)$$

With $r$ being Earth's radius (~6371km) and $(\varphi_2, \lambda_2)$ your point's latitude and longitude, respectively.

However, as stated before, that couldn't possibly give you a linear relation, as you can see by 3d plotting the function:

Implementation

The circumstances imply you're likely to be using pandas, or at least should be. Here's an example implementation of this relativized Haversine formula:

from math import radians, cos, sin, asin, sqrt

def single_pt_haversine(lat, lng, degrees=True):
    """
    'Single-point' Haversine: Calculates the great circle distance
    between a point on Earth and the (0, 0) lat-long coordinate
    """
    r = 6371 # Earth's radius (km). Have r = 3956 if you want miles

    # Convert decimal degrees to radians
    if degrees:
        lat, lng = map(radians, [lat, lng])

    # 'Single-point' Haversine formula
    a = sin(lat/2)**2 + cos(lat) * sin(lng/2)**2
    d = 2 * r * asin(sqrt(a)) 

    return d

Which could be used as in the below minimal example:

>>> import pandas as pd

>>> df = pd.DataFrame([[45.0, 120.0], [60.0, 30.0]], columns=['x', 'y'])
>>> df
      x      y
0  45.0  120.0
1  60.0   30.0

>>> df['harvesine_distance'] = [single_pt_haversine(x, y) for x, y in zip(df.x, df.y)]
>>> df
      x      y  harvesine_distance
0  45.0  120.0        12309.813344
1  60.0   30.0         7154.403197

Answer 2

The best practice is to not attempt to flatten Earth into a onee dimensional line... Because as you may know, Earth more resembles a sphere than a line. It is much better to treat it as such properly.

There do exist approaches to flatten a k-dimensional space into a one dimensional order though. These are known as space filling curves and are from the 19th century. Their limitations are well understood: for many points they will work quite well - but in other locations they work really badly. As known from complex number theory, you cannot find a good linear order of a plane.