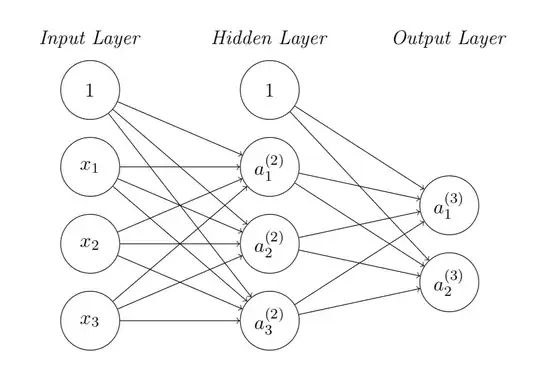
I’m new to machine learning and recently facing a problem on back propagation of training a neural network using ReLU activation function shown in the figure. My problem is to update the weights matrices in the hidden and output layers.
The cost function is given as:
$J(\Theta) = \sum\limits_{i=1}^2 \frac{1}{2} \left(a_i^{(3)} - y_i\right)^2$
where $y_i$ is the $i$-th output from output layer.
Using the gradient descent algorithm, the weights matrices can be updated by:
$\Theta_{jk}^{(2)} := \Theta_{jk}^{(2)} - \alpha\frac{\partial J(\Theta)}{\partial \Theta_{jk}^{(2)}}$
$\Theta_{ij}^{(3)} := \Theta_{ij}^{(3)} - \alpha\frac{\partial J(\Theta)}{\partial \Theta_{ij}^{(3)}}$
I understand how to update the weight matrix at output layer $\Theta_{ij}^{(3)}$, however I don’t know how to update that from the input layer to hidden layer $\Theta_{jk}^{(2)}$ involving the ReLU activation units, i.e. not understanding how to get $\frac{\partial J(\Theta)}{\partial \Theta_{jk}^{(2)}}$.
Can anyone help me understand how to derive the gradient on the cost function...?