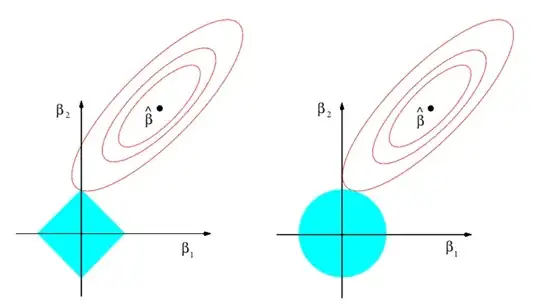
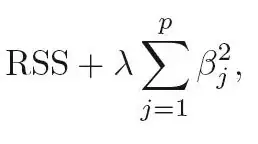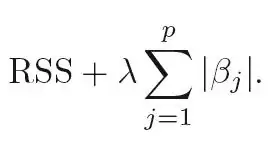Look at the penalty terms in linear Ridge and Lasso regression:
Ridge (L2):
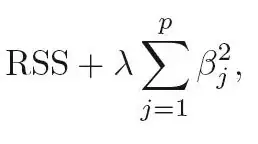
Lasso (L1):
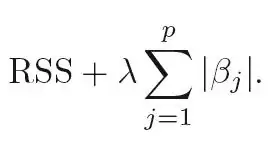
Note the absolute value (L1 norm) in the Lasso penalty compared to the squared value (L2 norm) in the Ridge penalty.
In Introduction to Statistical Learning (Ch. 6.2.2) it reads:
"As with ridge regression, the lasso shrinks the coefficient estimates towards zero. However, in the case of the lasso, the L1 penalty has the effect of forcing some of the coefficient estimates to be exactly equal to zero when the tuning parameter λ is sufficiently large. Hence, much like best subset selection, the lasso performs variable selection."
http://www-bcf.usc.edu/~gareth/ISL/