1

I couldn't figure out how it selected the root node with with <=7.5 and it's gini impurity is 0.45 but I tried to manually calculate it but the weighted gini impurity I got for it was 0.27.

Can anyone explain me how the calculation is done here just for the Root Node?

Here's a small dataset that I've generated,

import pandas as pd
import numpy as np

a = [5, 6, 7, 8, 9]
a1 = [1, 0, 1, 0, 0]
df = pd.DataFrame(np.c_[a, a1], columns=['val','target'])

   val  target
0    5       1
1    6       0
2    7       1
3    8       0
4    9       0

Here my code,

from sklearn.tree import DecisionTreeClassifier    
from IPython.display import Image
import pydot

dt = DecisionTreeClassifier()
dt.fit(df.val.to_frame(), df.target.to_frame())

data_dot = export_graphviz(dt, out_file=None, class_names=['0', '1'])
graph= pydot.graph_from_dot_data(data_dot)
Image(graph[0].create_png())

enter image description here

Jeeth
  • 911
  • 2
  • 10
  • 18

2 Answers2

2

From ISLR:

... we consider all predictors $X_1$, . . . , $X_p$, and all possible values of the cutpoint s for each of the predictors, and then choose the predictor and cutpoint such that the resulting tree has the lowest RSS ...

Since it's a classification problem, the best split is chosen by maximizing the Gini Gain, which is calculated by subtracting the weighted impurities of the branches from the original Gini impurity.

For c total classes with the probability of picking a datapoint with class, i is p(i), then the Gini Impurity is calculated as:

\begin{equation} G = \sum_{i=1}^{c} [ p(i) * (1 − p(i)) ] \end{equation}

1. Gini Impurity

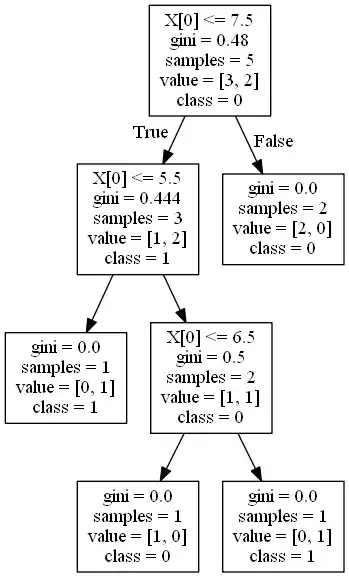
Here, c = 2 , P(0) = 3/5 and P(1) = 2/5

G = [P(0) * (1 - P(0))] + [P(1) * (1 - P(1))]

G = [3/5 * (1 - 3/5)] + [2/5 * (1 - 2/5)] = 12/25

G = 0.48

2. Gini Gain

Now, let's determine the quality of each split by weighting the impurity of each branch. This value - Gini Gain is used to picking the best split in a decision tree.
In layman terms, Gini Gain = original Gini impurity - weighted Gini impurities So, higher the Gini Gain is better the split.

Split at 6.5:

Gini Impurity G_left  = [1/2 * (1 - 1/2)] + [1/2 * (1 - 1/2)] = 0.50
Gini Impurity G_right = [2/3 * (1 - 2/3)] + [1/3 * (1 - 1/3)] = 0.44
Weighted Gini  = (1/5 * .50) + (4/5 * 0.44) = 0.45
Gini Gain = 0.48 - 0.45 = 0.03

Split at 7.5:

Gini Impurity G_left  = [2/3 * (1 - 2/3)] + [1/3 * (1 - 1/3)] = 0.444
Gini Impurity G_right = [2/2 * (1 - 2/2)] = 0
Weighted Gini  = (3/5 * 0.444) + (2/5 * 0) = 0.27
Gini Gain = 0.48 - 0.27 = 0.21

Split at 8.5:

Gini Impurity G_left  = [2/4 * (1 - 2/4)] + [2/4 * (1 - 2/4)] = 0.500
Gini Impurity G_right$ = [1/1 * (1 - 1/1)] = 0
Weighted Gini  = (4/5 * 0.5) + (1/5 * 0) = 0.40
Gini Gain = 0.48 - 0.40 = 0.08

So, the best split will be chosen 7.5 because it has the highest Gini Gain.

satznova
  • 161
  • 5
  • Thank you :)... – Jeeth Jul 20 '19 at 01:17
  • In this it calculates $\le 7.5$ but is it always the case? How does it selects whether to use $\gt$ or $\le$ or $\ge$ etc? Is it random in nature? – Jeeth Jul 20 '19 at 06:01
  • @user_6396 Hi, it won't be random. The values in the column will be sorted and only the mid-points between adjacent values will be considered for the split points. [Please ref here](https://datascience.stackexchange.com/questions/24339/how-is-a-splitting-point-chosen-for-continuous-variables-in-decision-trees) – satznova Jul 28 '19 at 15:10
1

The gini coefficient computed for each node is the one computed for all observations assigned to that node. So in the root node you have 2 ones and 3 zeros which leads to 0.49 as expected. To select the best split you compute the gini coefficients for both left and right nodes of instances and select the one which has the smallest sum of those coefficients

rapaio
  • 4,633
  • 20
  • 35
  • thank you ! In this it calculates $\le 7.5$ but is it always the case? How does it selects whether to use $\gt$ or $\le$ or $\ge$ etc? Is it random in nature? – Jeeth Jul 20 '19 at 06:02
  • Honestly, I do not remember if half interval between data points is a standard de facto. In my own implementations I prefer to add a little bit of randomness, especially when trees are in ensembles – rapaio Jul 20 '19 at 12:19