2

I was going through a paper comparing glove and word2vec. I came across the pound notation shown below. What does it mean when used like this? 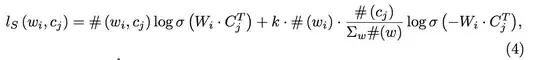equation The link for paper is here

Sagar Patel
  • 63
  • 1
  • 5

2 Answers2

2

In the third paragraph of the first section (page 1), they define $\#(w)$, $\#(w; c)$, and $\#(c)$. Quoting such paragraph:

Word-context pairs are denoted as $(w; c)$, and $\#(w; c)$ counts all observations of $(w; c)$ from the corpus. We use $\#( w ) = \sum_c \#(w; c)$ and $\#(c) = \sum_w \#(w; c)$ to refer to the count of occurrences of a word (context) in all word-context pairs. Either $\sum_c \#(c)$ or $\sum_w \#(w)$ may represent the count of all word-context pairs.

So, considering the equation you cited:

  1. $\#(w_i, c_j)$ counts the occurrences of a specific word $w_i$ over the context $c_j$;
  2. and $\frac{\#(c_)}{\sum_w \#(w)}$ accounts for the the probability of having context $c_j$ in the dataset.
Rubens
  • 4,097
  • 5
  • 23
  • 42
-1

That just means count. #(w) is the number of times w occurs in the corpus.

spikedlatte
  • 101
  • But for $$ #(w_i, c_j) $$ I couldnt figure out what it is because this is loss for a specific pair of words. So why count in there – Sagar Patel Apr 30 '15 at 17:18