In "Generalization and Network Design Strategies", LeCun argues that he chose parameters that satisfy:
$$ f (\pm1) = \pm1$$
The rationale behind this is that the overall gain of the squashing transformation is around 1 in normal operating conditions, and the interpretation of the state of the network is simplified. Moreover, the absolute value of the second derivative of $f$ is a maximum at $+1$ and $-1$, which improves the convergence at the end of the learning session.
Visualization of the derivatives using this code:
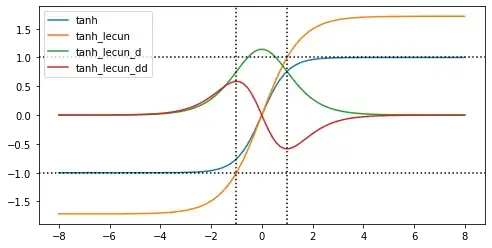
From his description of the maxima of the second derivative I conclude that the third differentiation of $f(x)=a*tanh(bx)$ should be zero for $ x = \pm1$. The third differentiation is:
$$\frac{\partial^{3} f}{\partial x^3}=\frac{-2ab³}{cosh²(bx)}\left(\frac{1}{cosh²(bx)} - 2tanh²(bx)\right) $$
So we set it to zero: $$1-2sinh²(bx)=0 \quad x\in\pm1$$
$$bx=arcsinh(\frac{1}{\sqrt{2}})$$
Plugging the values into numpy I get:
$$b=0.6584789484624083$$
Plugging the result into $f(1)$ I get:
$$a=1.7320509044937022$$
This means there is a slight difference in values between my variables and his. Comparing the the tanh using our different variable values I get $\delta = 0.0012567267661376946$ for $x=1$ using my numpy code.
Either I made a mistake, he did not have such an accurate numerical solver/lookup table, or he chose a "nicer looking" number.
