Confusion about the MSE ERROR

Question

I created a Random Forest regressor model and calculated my own error. I also want to calculate MAE, MSE and RMSE to compare my results to similar use cases. I am confused by the results as the values are far lesser.

The random forest regressor function I used is the default one. So I am just curious if there is anyone who can interpret my MAE, MSE, RMSE? Or did I do something wrong?

# Random Forest Regressor trainieren
random_state = 42

rf.fit(X_train, y_train)

These are the results of my own error:

Testset size: 19688
mean error(AVG): 0.10146151388130142
median error (Median): 0.061079373768676316

These are the results that look confusing to me:

# predict the testset
y_pred = rf.predict(X_test)


# Random Forest Basline Model evaluation
print('Mean Absolute Error:', metrics.mean_absolute_error(y_test, y_pred))  
print('Mean Squared Error:', metrics.mean_squared_error(y_test, y_pred))  
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))

#Mean Absolute Error: 0.027392195979941525
#Mean Squared Error: 0.00142917555312868
#Root Mean Squared Error: 0.03780443827288907

Answer 1

After giving much consideration, let's review the mechanism of Random Forest Regression (RFR):

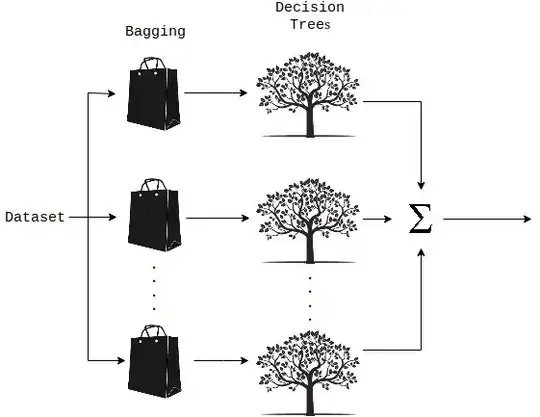
So this idea or process of averaging models is a technique called Ensembling. Additionally, Random forest is a Supervised Learning algorithm which uses an ensemble learning method for classification and regression. Random forest is a bagging technique and not a boosting technique. It uses a multitude of decision trees at training time and outputting the class that is the mode of the classes (classification) or mean prediction (regression) of the individual trees.

If you check sklearn documentation, the metrics for evaluation are:

• MSE (default) ---> Root of MSE ---> RMSE (optional)
• MAE ---> Percentage form of MAE ---> MAPE (optional)

Additionally, MSE is recommended to use on continuous data via this post

You can use the method of score(X, y): Return the coefficient of determination R^2 of the prediction.

The coefficient R^2 is defined as (1 - u/v), where:

• u is the residual sum of squares ((y_true - y_pred) ** 2).sum()
• v is the total sum of squares ((y_true - y_true.mean()) ** 2).sum()

The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse).

A constant model that always predicts the expected value of y, disregarding the input features, would get a R^2 score of 0.0.

The problem with this question is OP didn't share info about the evaluation of used metrics on the train and test datasets except for his own defined metric formula and some SKlearn metrics as follows:

#OP's defined metric #MSE
average_mean_error = (SalesPrice - predPrice) / Salesprice

result_rfbl.insert(2, "predResidualValue", rf.predict(X_test), True) 
result_rfbl.insert(2, "predPrice",  round(result_rfbl["predResidualValue"] * result_rfbl["NEUPREIS"], 2), True) 
result_rfbl.insert(2, "SalesPrice", round(result_rfbl["RESTWERT"] * result_rfbl["NEUPREIS"], 2), True) 

# absolute prozentualer Fehler #MAPE
result_rfbl.insert(2, "ERROR", abs(result_rfbl["SalesPrice"] - result_rfbl["predPrice"])/result_rfbl["SalesPrice"], True)

I assume that his model seems to be overfitting If validation MSE higher than the training MSE and get a very decent result with the training MSE nevertheless I don't want to judge by the cover of the book. If it is the case, RFR-model needs to apply feature engineering or RFR-analysis and Regularization like Ridge (L2 regularization) & Lasso (L1 regularization).

To understand better the reason behind the difference between manual defined MSE and Sklearn MSE, I draw your attention to minimum weighted MSE calculation for the first Split of a Decision Tree on SalesPrice from this source.