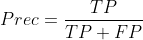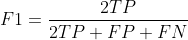Can the F1 score be equal to zero?

Question

As it is mentioned in the F1 score Wikipedia, 'F1 score reaches its best value at 1 (perfect precision and recall) and worst at 0'.

What is the worst condition that was mentioned?

Even if we consider the case of: either precision or recall is 0. The whole F1-score value becomes undefined. Because when either precision or recall is to be 0, true postives should be 0. When the true positives value becomes 0, both the precision and recall become 0.

also posted at https://stats.stackexchange.com/q/459549/232706 — Ben Reiniger, May 15 '20 at 15:18

score 7 · Answer 1 · edited Apr 11 '20 at 13:31

7

F1 will never be zero, but very near to zero for a bad classifier. If TP or TN is zero then there isn't any need to check F1.

edited Apr 11 '20 at 13:31

Peter Mortensen

155
5

answered Apr 10 '20 at 09:41

Gaurav Koradiya

257
1
8

score 5 · Answer 2 · answered Apr 10 '20 at 09:39

5

It's a mistake on Wikipedia.

$F_{1}$ as the harmonic mean is defined only at positive real numbers. $PRE$ or $REC$ could be equal 0 in case $TP=0$. Which provides to undefined result $F_1=\frac{0}{0}$.

answered Apr 10 '20 at 09:39

fuwiak

1,355
8
13
26

2

Have you added something to the talk page for that Wikipedia article (to point out mistake)? – Peter Mortensen Apr 11 '20 at 12:14

score 2 · Answer 3 · edited Apr 11 '20 at 13:01

It can't be exactly zero. We need exactly one (only one) of precision. Or recall to be zero to make f1 = zero, but both have "tp" as the numerator.

#### Will be Nan
y_test = np.array([0,0,1,1])
y_pred = np.array([0,1,0,0])

from sklearn.metrics import confusion_matrix
tn, fp, fn, tp = confusion_matrix(y_test, y_pred).ravel()
precision = tp/(tp+tn)
recall = tp/(tp+fn)
f1 = 2*precision*recall/(precision+recall)
print(f1)

nan

#### Can be ~0 with a specific case, with this data
y_test = np.hstack((np.zeros((1,2)),np.ones((1,1000000))))
y_pred = np.hstack((np.ones((1,1)),np.zeros((1,1000000)),np.ones((1,1))))
tn, fp, fn, tp = confusion_matrix(y_test[0], y_pred[0]).ravel()
precision = tp/(tp+tn)
recall = tp/(tp+fn)
f1 = 2*precision*recall/(precision+recall)
print('{0:1.6f}'.format(f1))

0.000002

Diamond · Answer 4 · 2021-07-23T14:11:45.113

1

If we go by the formula, it can actually be zero when when at least one of precision or recall is zero (regardless of the other one being zero or undefined). Look at the formulas for precision, recall, and F1:

$Prec=\frac{TP}{TP+FP}$

$Rec = \frac{TP}{TP+FN}$

$F1=\frac{2TP}{2TP + FP + FN}$

By looking at the F1 formula, F1 can be zero when TP is zero (causing Prec and Rec to be either 0 or undefined) and FP + FN > 0. Since both FP and FN are non-negative, this means that F1 can be zero in three scenarios:

1- TP = FP = 0 ^ FN > 0,

2- TP = FN = 0 ^ FP > 0,

3- TP = 0 ^ FP > 0 ^ FN > 0.

In the first scenario, Prec is undefined and Rec is zero. In the second scenario, Prec is zero and Rec is undefined, and in the last scenario, both Prec and Rec are zero.

edited Jul 23 '21 at 14:11

answered Jul 22 '21 at 11:56

Diamond

111
3

Ooh, +1. "Harmonic mean of precision and recall" is problematic when either is zero, but by expanding precision and recall to their confusion-matrix components, we fill in the removable discontinuity. Note that for this expanded version of F1 to be undefined, we need $TP=FN=0$, but that implies that there are no positive examples in the dataset, quite a degenerate problem. – Ben Reiniger Jul 22 '21 at 15:04
@BenReiniger: Thanks for your comment. I updated my answer. TP = FN = 0 does not necessarily mean that F1 is undefined; FP should also be zero; otherwise, F1 would be zero. – Diamond Jul 23 '21 at 14:59
yes, I was only stating the one directional implication. – Ben Reiniger Jul 23 '21 at 15:29
Oh, yeah, in that case, you're absolutely correct. – Diamond Jul 23 '21 at 17:50

Can the F1 score be equal to zero?

4 Answers4