High error Arima model - Python

Question

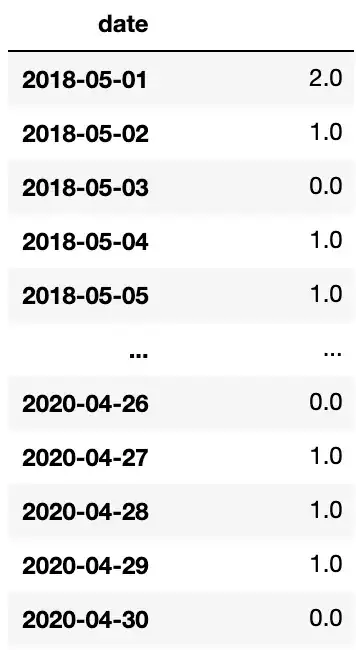
I have a time series data. It has daily frequency.

I want to forecast the data for the next week or month with an ARIMA model.

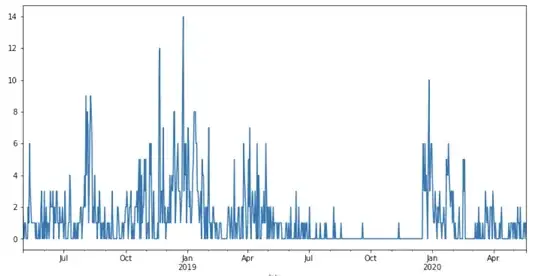
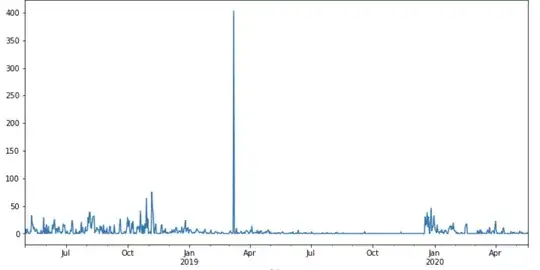
This is a chart of my time series data:

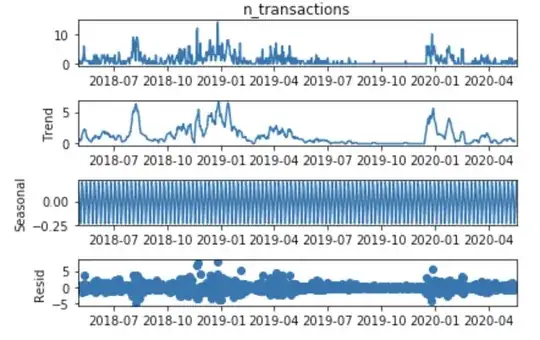
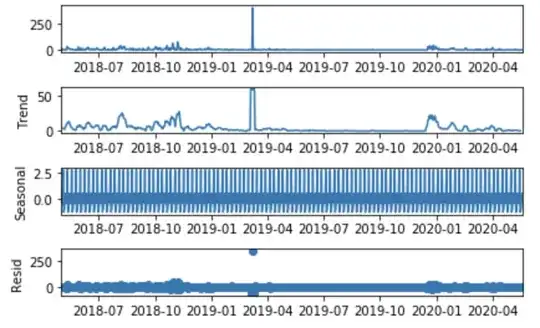
First I use the method seasonal_decompose from stats model to check the trend/sessionality/residual looks like:

from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(df['n_transactions'], model='add')
result.plot(); 

I check if my data is stationary:

from statsmodels.tsa.stattools import adfuller

def adf_test(series,title=''):
    """
    Pass in a time series and an optional title, returns an ADF report
    """
    print(f'Augmented Dickey-Fuller Test: {title}')
    result = adfuller(series.dropna(),autolag='AIC') # .dropna() handles differenced data

    labels = ['ADF test statistic','p-value','# lags used','# observations']
    out = pd.Series(result[0:4],index=labels)

    for key,val in result[4].items():
        out[f'critical value ({key})']=val

    print(out.to_string())          # .to_string() removes the line "dtype: float64"

    if result[1] <= 0.05:
        print("Strong evidence against the null hypothesis")
        print("Reject the null hypothesis")
        print("Data has no unit root and is stationary")
    else:
        print("Weak evidence against the null hypothesis")
        print("Fail to reject the null hypothesis")
        print("Data has a unit root and is non-stationary")

adf_test(df['n_transactions'])

Augmented Dickey-Fuller Test: 
ADF test statistic       -3.857922
p-value                   0.002367
# lags used              12.000000
# observations          737.000000
critical value (1%)      -3.439254
critical value (5%)      -2.865470
critical value (10%)     -2.568863
Strong evidence against the null hypothesis
Reject the null hypothesis
Data has no unit root and is stationary

I use auto_arima in order to get the best parameters for my model:

from pmdarima import auto_arima      
auto_arima(df['n_transactions'],seasonal=True, m = 7).summary()

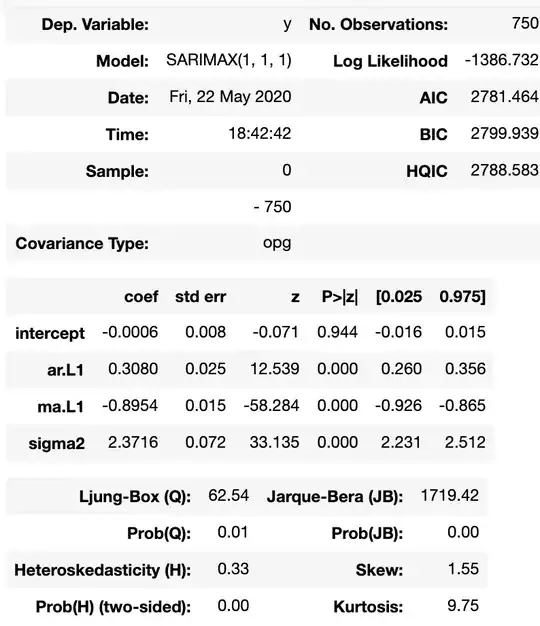
I train my model with this paremeters:

train = df.loc[:'2020-05-12']
test = df.loc['2020-05-13':]

model = SARIMAX(train['n_transactions'],order=(1, 1, 1))
results = model.fit()
results.summary()

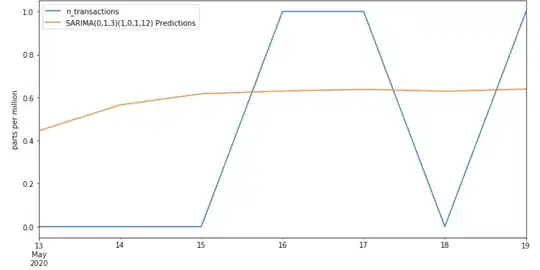
I calculate the predictions:

start=len(train)
end=len(train)+len(test)-1
predictions = results.predict(start=start, end=end, dynamic=False, typ='levels').rename('SARIMA(0,1,3)(1,0,1,12) Predictions')


ax = test['n_transactions'].plot(legend=True,figsize=(12,6),title=title)
predictions.plot(legend=True)
ax.autoscale(axis='x',tight=True)
ax.set(xlabel=xlabel, ylabel=ylabel);

But the model can't obtain good results, why?

Edit

I have used instead of counts the revenue that I obtain for this counts as you suggested me that may be this would be the problem:

But the model is not obtaining good results:

What conclusion can I extract from here?

Answer 1

your data looks like a count process. The default ARIMA parameters assume a normal distributed continues error term. So the standard ARIMA models are using this assumption. As far as I know there are some ARIMA models with poisson distribution as an error term, but I guess you just should google for timeseries for count processes. Something like pyflux could work.

Answer 2

You seem to have a time series of counts. Quoting from book above:

All of the methods discussed in this book assume that the data have a continuous sample space. But often data comes in the form of counts. For example, we may wish to forecast the number of customers who enter a store each day. We could have 0, 1, 2, , customers, but we cannot have 3.45693 customers.

The author suggest an approach using Croston's methods, usually applied to time series with high number of zeros.