6

I am studying machine learning, and I have encountered the concept of bias and variance. I am a university student and in the slides of my professor, the bias is defined as:

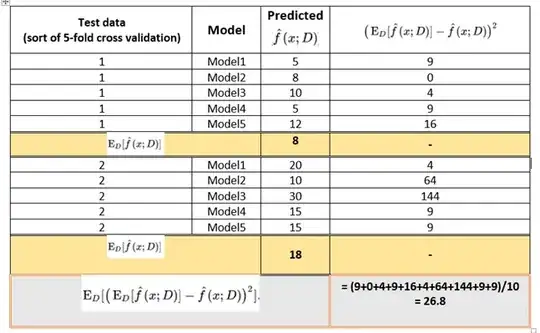
$bias = E[error_s(h)]-error_d(h)$

where $h$ is the hypotesis and $error_s(h)$ is the sample error and $error_d(h)$ is the true error. In particular, it says that we have bias when the training set and the test set are not independent.

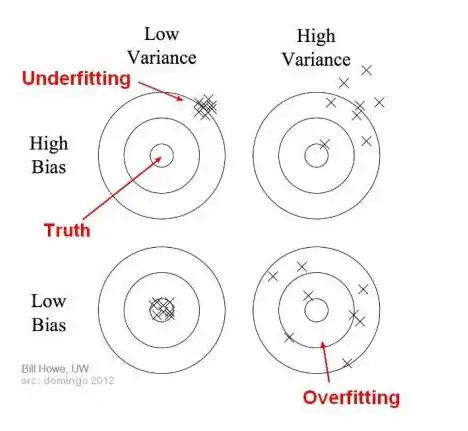
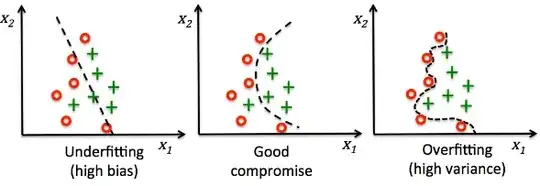
After reading this, I was trying to get a little deeper in the concept, so I searched on internet and found this video , where it defines the bias as the impossibility to capture the true relationship by a machine learning model.

I don't understand, are the two definition equal or the two type of bias are different?

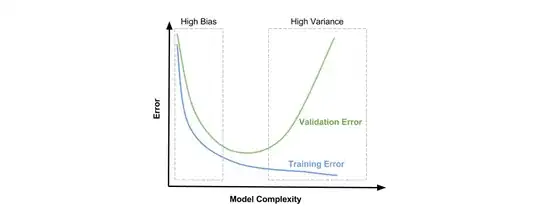
Together with this, I am also studying the concept of variance, and in the slides of my professor it is said that if I consider two different samples from the sample, the error may vary even if the model is unbiased, but in the video I posted it says that the variance is the difference in fits between training set and test set.

Also in this case the definitions are different, why?

Andrew Kelley
  • 103
  • 3
J.D.
  • 841
  • 4
  • 15
  • 29

3 Answers3

10

What are Bias and Variance?

Let's start with some basic definitions:

  • Bias: it's the difference between average predictions and true values.
  • Variance: it's the variability of our predictions, i.e. how spread out your model predictions are.

They can be understood from this image:

enter image description here

(source)

What to do about bias and variance?

If your model suffers from a bias problem you should increase its power. For example, if the prediction of your neural network is not good enough, add more parameters, add a new layer making it deeper, etc.

If your model suffers from a variance problem instead, the best possible solution is coming from ensembling. Ensembles of Machine Learning models can significantly reduce the variance in your predictions.

The Bias-Variance tradeoff

If your model is underfitting, you have a bias problem, and you should make it more powerful. Once you made it more powerful though, it will likely start overfitting, a phenomenon associated with high variance. For that reason, you must always find the right tradeoff between fighting the bias and the variance of your Machine Learning models.

enter image description here

(source)

Learning how to do that is more an art than a science!

Leevo
  • 6,005
  • 3
  • 14
  • 51
  • 1
    What exactly do the bulleyes and the points on the bulleye diagram represent? I get that it's (probably) the error of individual predictions, but isn't that usually one-dimensional? Or is it just an abstract picture intended to convey an idea rather than being a concrete representation of some data? – NotThatGuy Aug 12 '20 at 22:18
  • The bullseys are hypothetical Loss functions, with the center being the global minimum to be reached. But you can think of them as *actual* bullseys, and the points being shots. – Leevo Aug 13 '20 at 14:02
1

I am attaching below a screen shot of calculations performed to explain the definition of variance in Wikipedia.

Create 5-models from 5-different training datasets (similar to but not exactly, 5-fold cross-validation). That is prepare 5-models from differing training datasets. To each model, feed the same test data. Our test-data has two observations. Below are the results of predictions and calculations of variance. Extent of variance is 26.8

enter image description here

Ashok K Harnal
  • 111
  • 3
0

Well this image explains it all : in ML, you have a bias/variance dilemma : you want to create a model that is precise-enough to learn things from your data, but not perfectly-precised so it learns a tendancy and not the exact values of your training set.

Variance and Bias are to be taken together : on a same model, when you tweak to lower Variance, you'll automatically increase Bias.

Your job is then to get the good compromise, as show in image : a variance high enough (ie a bias low enough) to make good predictions and learn something from your train, but not a too high variance (ie not a too low bias) to avoid overfitting.

enter image description here

Adept
  • 854
  • 5
  • 17
  • The image explains it fairly well to me (who already understands it), but an explanation could still help others who may not quite be seeing what you're seeing in the image (or if they're unable to view the image for whatever reason). The rest of your answer mostly addresses the tradeoff (kind of) between bias and variance rather than what they mean. – NotThatGuy Aug 12 '20 at 22:26
  • The answer was more about practical understanding of what bias and variance represent in machine learning, than what it is mathematically and theorically, which I'm not prefectly aware of – Adept Aug 13 '20 at 08:02
  • It doesn't have to involve mathematics or too much theory. If you assume someone reads this answer and they're unable to see or interpret the image, do you believe they would learn what bias and variance means based on the text alone? The text seems to assume the reader already knows what bias and variance is. [The other answer](https://datascience.stackexchange.com/a/80161/90951) could potentially serve as a good example of what I mean: there are images, but the answer doesn't rely on them. – NotThatGuy Aug 13 '20 at 11:08