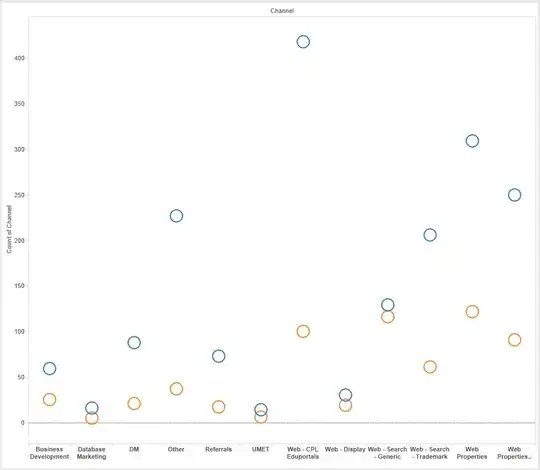
We first have the weights of a D dimensional vector $w$ and a D dimensional predictor vector $x$, which are all indexed by $j$. There are $N$ observations, all D dimensional. $t$ is our targets, i.e, ground truth values. We then derive the cost function as follows: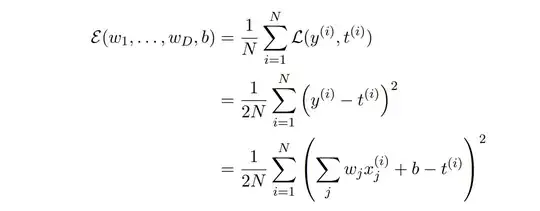 
We then compute the partial derivate of $\varepsilon$ with respect to $w_j$: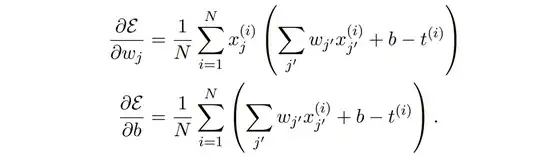 
I'm confused as to where the $j'$ is coming from, and what it would represent.
We then write it as:
Then, we vectorize it as:
I'm confused as to the derivation of the vectorization of $A$ from $A_{jj'}$ likely because I don't know what $j'$ is. But how would the vectorization go in terms of steps and intuition?
Here is the link to the handout.
