4

I'm writing a data science report, I want to find an exist distribution to fit the sample. I got a good looking result cdf pdf, but when I use KS-test to test the model, I got a low p-value,1.2e-4, definitely I should reject the model.

I mean, whatever what distribution/model you use to fit the sample, you cannot expect to have a perfect result, especially working with huge amount of data. So what does KS-test do in a data science report? Does it means only if we got high p-value in KS-test then the model is correct?

Carl
  • 51
  • 2
  • 1
    this must be a stupid question, in real world, do we always be able to find a fitting curve with high enough p-value? And what if we can't, then we have to disprove our assumption? – Carl Feb 12 '21 at 20:27
  • In my sole opinion: I do use to measure the discriminatory power of the model, In other words if my model does distinguish between events and non-events(looking at first 4 deciles). In this way KS I do use for model selection aka what model does perform better for my problem/task I try to solve (not only logit models). And I do use on the large amount of data (hundreds of millions of obs) ... on what u do show is to test if your data comes from same distribution and I do not see usage on validating model performance ... if u agree With my approach I will post detailed answer. – n1tk Feb 13 '21 at 16:17
  • 1
    There is no contradiction. Your chosen distribution is a pretty good fit. The low p-value (loosely speaking) says that it is not a perfect fit. If you have a fairly large sample size, then you have the sensitivity to detect even small deviations from the fitted distribution. You might be interested in this discussion over at the statistics Stack: https://stats.stackexchange.com/q/2492/247274. – Dave Apr 14 '21 at 10:13

2 Answers2

0

In your case, the null hypothesis $H_0$ is that your sample follows your the distribution that your model has learned. The alternative hypothesis $H_1$ is that it follows some other distribution. Assuming you have fixed your significance level $\alpha$ to be $0.05$ (the most common choice for $\alpha$, but up to you if you want to go lower), getting a p-value lower than that means you should reject the null hypothesis.

The p-value can be interpreted as the probability of a type I error, in other words a false positive: the probability that you reject the null hypothesis when it is in fact true. In your case, rejecting the hypothesis means stating that there is statistically significant evidence that the distribution your model has learned is not the underlying distribution of the sample. So yes, you would like as large a p-value as possible.

You are using a Kolmogorov-Smirnov test to compare your sample to a reference distribution, in this case, so it's a one-sample KS test. The way I would put it is that getting a high p-value means that: "it is highly unlikely that your model has learned a wrong distribution". In other words, it is highly likely it has learned a pretty good approximation of the underlying distribution. However, nothing is certain when doing statistical hypothesis testing!

I'm not sure what you're showing on your plots though, since there doesn't seem to be an empirical cumulative distribution function on them (lines look smooth).

David Cian
  • 201
  • 1
  • 5
  • 1
    Yeah, I think I understand the meaning of p-value. To clarify, I used two Pareto distribution to form an empirical distribution and find the parameters by maximum likelihood, and the blue line in first plot is the sample's CDF, and the red line is the fitting CDF. What confused me is, even if I used log scale when plotting, this empirical distribution seem fit the sample great, but I still got a pretty low p-value. So in this case, I should change my assumption to find other distribution to fit the sample? – Carl Feb 12 '21 at 19:40
  • The test statistic of the KS test is the Kolmogorov Smirnov statistic, which is the greatest distance between your empirical and predicted distributions. The test statistic of a test is itself assumed to follow a distribution "in the wild", here the Kolmogorov distribution. The p-value is defined (here, for a one-sided right-tail test) as the probability of something more extreme (i.e. distance between the two distributions even greater). One weakness of the KS test is few & far between data points, which leads to large KS statistic which leads to low p-value. How many data points do you have? – David Cian Feb 13 '21 at 00:09
  • When you're saying "empirical distribution" do you mean you sampled the two Pareto distributions to give a discrete set of samples or just used them as is? – David Cian Feb 13 '21 at 00:10
-1

The p-value is interpreted as the probability of a type I error. In other words a false positive: the probability that you reject the null hypothesis when it is in fact true.

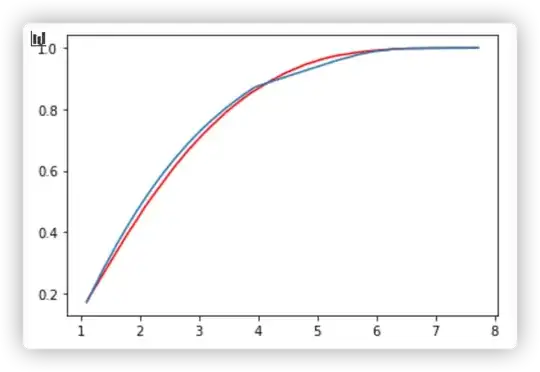
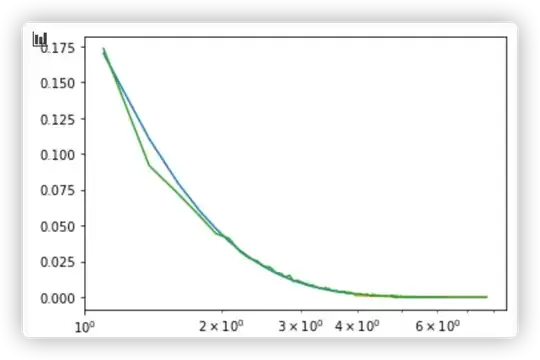You are invoking a Kolmogorov-Smirnov test.

" when I use KS-test to test the model, I got a low p-value,1.2e-4, definitely I should reject the model." Answer - Your low p-value does not indicate that the proposed model should be rejected. p value simply indicates the chance for comiting type - 1 error which is quite low in your case. The low value of p i.e. alpha implies that your model predicts very well. In nutshell, the test confirms correctness of your model.

Does it mean only if we got high p-value in KS-test then the model is correct? - "No".

Subhash C. Davar
  • 578
  • 4
  • 18
  • 2
    -1 The p-value, loosely speaking, is the probability of getting the observations you got if the null hypothesis is true. Thus, the low p-value is evidence against the null hypothesis. – Dave Apr 14 '21 at 10:08
  • @Dave p reflects chance of rejecting a null hypothesis when it is true. A low p-value implies a very little chance of rejecting the null hypothesis. It means a high goodness-of-fit between two distributions. Please re-check your interpretation. – Subhash C. Davar Mar 15 '23 at 01:01
  • 1
    A low p-value is evidence against the null hypothesis in favor of the alternative hypothesis. If the null hypothesis is that two distributions are the same, a low p-value thus disputes such a notion and provides evidence that the distributions are different. – Dave Mar 17 '23 at 10:57
  • If computed p-value is less than alpha set (say .05, it is in favour of null hypothesis. the null hypothesis is accepted Two distributions do not differ substantively. Note:The probability of committing a type I error (rejecting the null hypothesis when it is actually true) is called α (alpha) the other name for this is the level of statistical significance – Subhash C. Davar Mar 17 '23 at 23:30
  • Sorry, that’s totally incorrect. – Dave Mar 18 '23 at 00:20