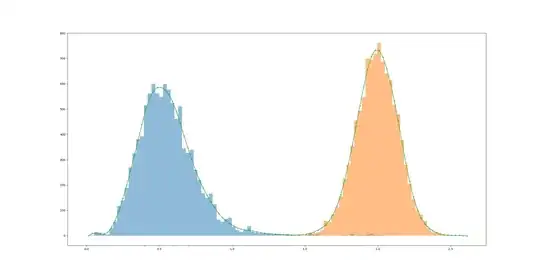
I am currently working on the titanic dataset from Kaggle. The data set is imbalanced with almost 61.5 % negative and 38.5 positive class.
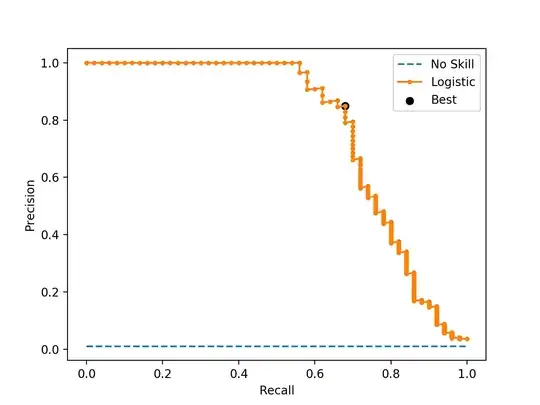
I divided my training dataset into 85% train and 15% validation set. I chose a support vector classifier as the model. I did 10-fold Stratified cross-validation on the training set, and I tried to find the optimal threshold to maximize the f1 score for each of the folds. Averaging all of the thresholds obtained on the validation folds, the threshold has a mean of 35% +/- 10%.
After that, I test the model on the validation set and estimated the threshold for maximizing F1 score on the validation set. The threshold for the validation set is about 63%, which is very far from the threshold obtained during cross validation.
I tested the model on the holdout test set from Kaggle and I am unable to get a good score for both of the thresholds (35% from cross-validation of train set and 63% from the validation set.)
How does one determine the optimal threshold from the available dataset which could work well on unseen data? Do I choose the threshold obtained from cross-validation or from the validation set? or am I doing it completely wrong? I would appreciate any help and advice regarding this.
For this Dataset, I am looking to maximize my score on the scoreboard by getting the highest accuracy.
Thank you.