41

I saw this graph about the global temperature, it goes back for 2000 years.

How is it possible to measure temperature 2000 years back with such a precision of like ~0.1 C?

The image from Reddit post I don't know the source of original data.

What tools are used to measure it?

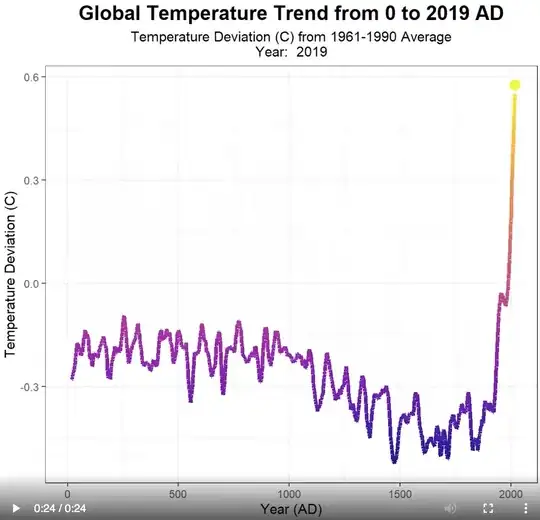
enter image description here

Alex Craft
  • 521
  • 1
  • 4
  • 7
  • 1
    There are several ways, for example https://en.wikipedia.org/wiki/Paleoclimatology#Proxies_for_climate. In order not to guess and tailor the answer to the case, what's the source of your graph ? –  Aug 23 '20 at 13:21
  • @a_donda Thanks, I added the link to the post on Reddit where the image is from, but I don't know what's the source of the original data. – Alex Craft Aug 23 '20 at 13:24
  • 4
    Does this answer your question? How accurate are climate proxies in giving us a clear picture of global average temperatures throughout Earth history? – jeffronicus Aug 23 '20 at 14:31
  • @jeffronicus thanks, partially. Do you know if those measures have precision shown on this chart, like ~0.1C? – Alex Craft Aug 23 '20 at 20:26
  • @AlexCraft Yes, but the methodology is probably a separate question. Following the chain of references from the Reddit post, the source of the data is the paper "A global multiproxy database for temperature reconstructions of the Common Era" (Nature) https://www.nature.com/articles/sdata201788, by the PAGES 2k consortium (http://pastglobalchanges.org/), an international scientific group which has been working to collect, organize, and analyze this data from multiple sources since 2008. – jeffronicus Aug 24 '20 at 15:25
  • 2
    Precision is not the same as accuracy. I can guess that you spent $75.01 on coffee this year. That's a very precise amount, but that does not mean it is accurate. You've pointed out the precision of that graph, but you have not pointed out (nor does the graph itself state) that is it provably accurate. – Flater Aug 24 '20 at 15:37
  • I think this is it: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6675609/, it refers to a 2019 Nature paper https://www.nature.com/articles/s41561-019-0400-0 that wraps a statistic around several global records. –  Aug 24 '20 at 15:58
  • 1
    What does the vertical axes label mean? Deviation from what ? Its consistently negative until sometime in the last century. – Criggie Aug 26 '20 at 01:57
  • A possible original picture, with uncertainties, is available here: https://en.wikipedia.org/wiki/File:T_comp_61-90.pdf coming from a paper published in 1999 ( https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/1999GL900070 ) – EarlGrey Aug 26 '20 at 06:59
  • @Flater Note also the difference between precision and resolution. The former is related to random deviation of repeated measurement of the same value at the same conditions ( several measurements of the room length by a ruler may provide different values, with the true value and standard deviation estimations ) , while the latter is related to the smallest distinguishable value of the measurement ( We can distinguish milimetres). – Poutnik Nov 10 '20 at 13:34

2 Answers2

55

How it's possible to measure temperature 2000 years ago?

Sans the technology used by Bill and Ted ("Bill and Ted's Excellent Adventure"), it obviously is not possible to directly measure the temperature from yesterday, let alone 2000 years ago, or longer. What is used are "proxies", things that can be measured today that serve as stand-ins for things such as temperature in the past.

One example of a proxy is the amount of oxygen-18 in the ice in Greenland and Antarctica. Water with two hydrogen atoms and one oxygen-16 atom has a boiling point of about 100° C. Water with the oxygen-16 atom replaced by an oxygen-18 atom has a slightly higher boiling point. This means that heavy oxygen water evaporates less readily but precipitates more readily than does normal water.

This in turn means that the fraction of oxygen 18 versus oxygen 16 in the water and air bubbles in the ancient ice in Greenland and Antarctica are indicative of the climate at the time that that ice and those air bubbles formed. Despite being a half a world apart, the ratios of oxygen-18 to oxygen-16 over time are highly consistent between Greenland and Antarctica. The consistency of these measures at half a world apart are almost universally taken as being a proxy for something else, and that something else is climate.

There are many other proxies for past climate. There are other isotopes that serve as proxies. The amounts and kinds of pollen in mountain glaciers and ice sheets form yet another kind of proxy. The kinds of plants that do grow in some locales and how fast they do grow is highly temperature dependent. Like ice, buried muds in the oceans also show variations in various proxies. Climate scientists put these proxy measurements together to arrive at the temperatures from 2000 years ago, and even further into the past.

David Hammen
  • 23,587
  • 1
  • 60
  • 102
  • Thanks, can you please add a note about the precision? The graph I refer to produces temperature with like 0.1C details? Is such a high precision possible for get via proxy-measures? – Alex Craft Aug 23 '20 at 20:25
  • 6
    @AlexCraft The graph is showing deviation, not absolute temperature. Statistical measurements like that can be produced to arbitrary accuracy provided you end up with the same number of significant digits as the original data set, and 0.1 is well within the likely number of significant digits for those original proxy measurements. – Austin Hemmelgarn Aug 23 '20 at 23:01
  • 4
    @Alex Craft: It should be possible to find graphs with error bars. I'm sure I've seen them, but don't remember where. – jamesqf Aug 24 '20 at 03:04
  • 1
    @AlexCraft Uncertainty propagation is a rather advanced mathematical topic. If the precision of the input data is known then the precision of the result can be calculated using the same model that produced the result from the input data. – J... Aug 24 '20 at 11:45
  • @J... It's even more advanced than that. A single proxy by itself yields a somewhat unclear picture of the past. Past climate is inferred from multiple proxies that some claim collectively support a more clear picture. Others (maybe a few others?) disagree, claiming that the uncertainties should from multiple proxies add to the uncertainty rather than reduce it. I've superficially read several of the papers that argue each way. I am not qualified to judge in this field, but in fields where I am qualified to judge, the more measurements the merrier. Particularly different kinds of measurements. – David Hammen Aug 24 '20 at 11:55
  • 6
    This is a good answer, but it could be improved by adding sources. And as a pedantic note, any temperature measurement is technically a proxy, just the paleoclimatological measurement is more steps away from the measurand than your electronic or analogue thermometre (although a global average temperature estimate still needs significant processing). – gerrit Aug 24 '20 at 12:21
  • @DavidHammen Not really, it's still an uncertainty propagation - the complexity of the model doesn't change the mathematical techniques that are used. Certainly some models are more difficult to produce analytical uncertainties for, and much of the debate on that topic it's still really about how good our understanding is of the proxies, what their exact roles are/were, and what interdependencies may exist betwen those proxies - because all of those things affect how you formulate the model and the uncertainties generated from each input. At the end of the day, it's still all error analysis. – J... Aug 24 '20 at 13:05
  • ISTM that if two proxies' error margins are dependent on each other, the margin on the final value ought to be a function of either one, and the calculation from either should yield an identical margin. If one proxy depends on another and also introduces additional error, the function of the dependent proxy ought to determine the final error. If the proxies are completely independent, then the final error is... unclear to me. My guess is a smaller error, but if the proxies each produce a different measurement, then I think something was broken earlier. How close am I? – Paul Brinkley Sep 03 '20 at 14:37
3

Your graphic shows temperature anomalies. That is, an average temperature is calculated over a large time frame, say 15 ° C. Then each value on the graphic is the CHANGE from that average. Anomalies are nice because "inaccurate" measurement instruments (proxies) can be used. An absolute reading can be off but the reading to reading change will be much more accurate, and other inaccurate instruments can be combined. Regarding precision and uncertainty. What your graphic is showing is an expected value, which can be as "precise" as you want it to be. It is only an expected value. Consider a pair of dice. The expected value is 7, but the roll of the dice can be anywhere from 2 to 12. Of more importance is uncertainty. This is not shown in your graphic. We "expect" a certain value but we are unsure as to exactly what we will measure each time. And now we get into probabilities and distributions. Another key to low uncertainty data is a lot of measurements or a lot of proxies. Some examples of graphics with associated uncertainties are Marcott 2013, Loehle 2008, and Kaufman 2020. I believe Marcott uses 75 or so proxies. Of course present global temperature data use thousands of measurements, which drives down the uncertainty.

Frank Mlinar
  • 31
  • 1