1

Assume two vertical pistons with their flat head facing upward.

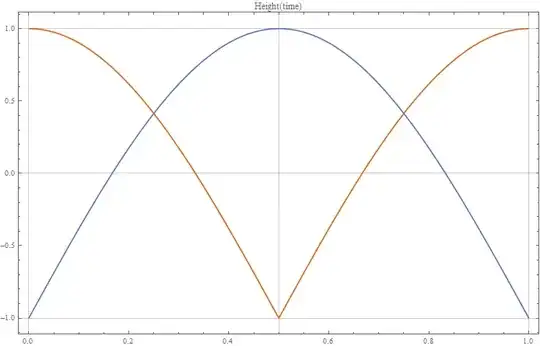
Is it possible to couple them to one rotating shaft in a way that the position vs. time diagram gets like this? (This is one complete cycle)

diagram

Each color being representing a piston.

The equations are:

Red: $$2 \left|\cos(\pi t)\right| - \frac12$$

Blue: $$2 \left|\sin(\pi t)\right| - \frac12$$ (The first with a phase difference of $\pi \over 2$)

I think because of the Absolute values, this can not be a simple crankshaft.

Can anyone help?

EDIT:

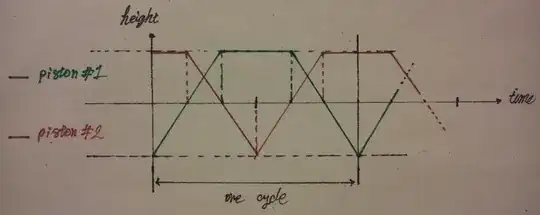
Actually I want to get as close as possible to this diagram of motion, which is the ideal theoretical case. Maybe this can help you for a better approximation.

real thing

AHB
  • 111
  • 3
  • 5
    That instantaneous velocity direction change is a killer. would require infinite acceleration. – joojaa Jan 19 '17 at 16:59
  • @joojaa Then we could soften the edge so that it becomes seamless. Would $\sin^2(\pi t)$ be fine enough? Is sin squared motion possible to be achieved using mechanical structures? – AHB Jan 19 '17 at 17:55
  • How exact do you need to be with any of this? A little insight as to why they have to have that position profile could help. – JMac Jan 19 '17 at 18:09
  • @JMac I added what you want. – AHB Jan 19 '17 at 18:32
  • You can do a lot with [4-bar linkages](http://engineering.stackexchange.com/a/13213/86). Note that the vertical movement of the feet (ignoring the horizontal movement) is very close to the profile you're looking for. – Dave Tweed Jan 20 '17 at 13:29
  • @DaveTweed I asked the math-related part of the question here: http://math.stackexchange.com/questions/2104888/what-would-be-the-smoothest-practical-approximation-for-this-diagram-position-o and Ross Millikan said something that caught my attention. Circles joined to circles, will this be practical? He explains how the mechanism will work but I didn't understand a word. – AHB Jan 20 '17 at 14:55
  • I briefly considered Fourier synthesis, but it would be a very complex mechanical arrangement, and more importantly, with a truncated series, the motion would generally be non-monotonic (the flat part would have oscillations in it), which I'm guessing would be a non-starter for your application. – Dave Tweed Jan 20 '17 at 23:06
  • @ABH yes its a cycloid observed from outside. – joojaa Jan 25 '17 at 05:24

1 Answers1

1

You can (come close to) this motion profile with two cams on one shaft. the tops being the dwell portion of the cams, and the bottom being the peak between two accelerations. As some one else mentioned since the bottom of your motion profile is an instantaneous acceleration change, you will never achieve it perfectly. this can be minimized by reducing mass, speed, and stroke length. This is going to be the closest mechanical way to do this.

Patstep
  • 11
  • 1
  • It would be best to machine the cams with smooth lead-ins and lead-outs either side of the sharp acceleration point. This would reduce wear and tear due to shock and vibration. –  Nov 24 '17 at 14:49