3

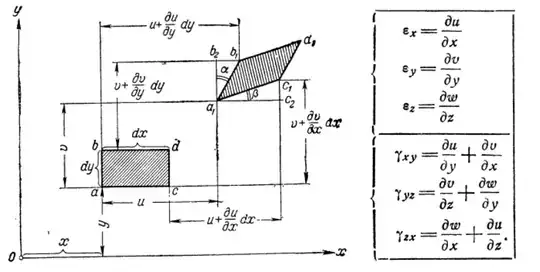
As you know in linear theory of elasticity equations for strains are given as (according to picture): enter image description here

But what will be if an element will just rotate (strain equation is on the picture): rotation of an element

Intuitively i think there should be no strains. The main question is how to deal with it?

Eugene
  • 73
  • 2
  • On mobile so can't give full answer, but look up Mohr's circle. You'll have individual strains in both x and y, but you will find one axis x' and y' where you can define no strain. – Mark Jun 10 '17 at 14:59
  • I'm guessing you're looking for [torsion](https://en.m.wikipedia.org/wiki/Torsion_(mechanics)). – JMac Jun 10 '17 at 15:47
  • In the first picture, the equations for the strain use engineering strain which is only valid for small rotations. So in the second picture, $\cos \varphi$ is small (approximately $\cos\varphi = 1 - \frac 1 2 \varphi^2$) and the second-order term $\varphi^2$ is ignored. So $\epsilon_x = 0$. If you want to model large rotations, use Green strain, not engineering strain, and you will get $\epsilon_x = 0$ exactly, for any value of $\varphi$. – alephzero Jun 10 '17 at 20:11

2 Answers2

3

The answer to this lies in the defining equation for the strains that you have supplied. The full displacement gradient $u_{i,j}$ (where the $\bullet_{,j}$ represents the $j^{\rm th}$ derivative) can be linearly decomposed into a symmetric and an anti-symmetric component: $u_{i,j} = \epsilon_{i,j} + \omega_{i,j}$, in the usual way as for all rank-2 tensors.

The symmetric part, $\epsilon_{i,j} = \frac{u_{i,j}+u_{j,i}}{2}$ represents the strain, the only thing that counts for elastic energy, whereas the anti-symmetric part $\omega_{i,j} = \frac{u_{i,j}-u_{j,i}}{2}$ represents rigid body rotation. And as you remarked, this costs no energy to the system. Hence, for elasticity, we only ever talk about $\epsilon_{i,j}$.

ap21
  • 163
  • 6
1

From your picture, your deformation map would be something like

$$ \varphi(x) = \left[\begin{array}{c} xcos(\varphi) - ysin(\varphi) \\ xsin(\varphi) + ycos(\varphi) \\ z \\ \end{array}\right] $$ Deformation gradient $$ F = \left[\begin{array}{ccc} cos(\varphi) & -sin(\varphi) & 0 \\ sin(\varphi) & cos(\varphi) & 0 \\ 0 & 0 & 1\\ \end{array}\right] $$ Green deformation tensor $$ G = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\\ \end{array}\right] $$ $$ \therefore E = \frac{1}{2} [G - I] = 0 $$ Which is what we would expect, but in order to calculate this we needed to use higher order terms. Since: $$ G = FF^T = (\nabla u + I)(\nabla u + I)^T = \nabla u + \nabla u^T + \nabla u \nabla u ^T + I $$ If each component of: $$ \nabla u < 1 $$ then each component of: $$ \nabla u \nabla u ^T \ll 1 $$ We expect our $\varphi$ to be very small, so we can ignore our higher order terms. Let's linearize the deformation gradient: $$ cos(\varphi) \approx 1, sin(\varphi) \approx \varphi \\ F = \left[\begin{array}{ccc} 1 & -\varphi & 0 \\ \varphi & 1 & 0 \\ 0 & 0 & 1\\ \end{array}\right] \\ G = \left[\begin{array}{ccc} 1 + \varphi ^2 & 0 & 0 \\ 0 & 1 + \varphi ^2 & 0 \\ 0 & 0 & 1\\ \end{array}\right] \\ \therefore E = \frac{1}{2} \left[\begin{array}{ccc} \varphi ^2 & 0 & 0 \\ 0 & \varphi ^2 & 0 \\ 0 & 0 & 0\\ \end{array}\right] \approx 0 $$ This makes since, because if $\varphi$ is small, $\varphi^2$ is much smaller and we can accept the error assuming geometrically linear behavior. We just need to watch out for non-small rotations that will cause our linearization to have a larger error.

Resource:

Fundamentals of Structural Mechanics 2nd, Keith D. Hjelmstad

WretchedLout
  • 161
  • 3