How to integrate ∫vᵢ(uᵢ² + vᵢ²)dA in calculating monosymmetry index of an angle?

Asked Jul 19 '17 at 10:44

Active Mar 06 '18 at 16:05

Viewed 248 times

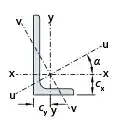
I saw this question asking about calculating monosymmetry index of an unequal angle. What I need is a formula to calculate $\int v_i{(u_i}^2 + {v_i}^2)\text{d}A$, given the depth $d$, breadth $b$ and thickness $t$ of an angle. $A$ is the area and $v$ and $u$ are the coordinates of each small element $i$ of the section. Is there a simplified method to derive the above, neglecting root radius and toe radius?

edited Jul 25 '17 at 05:51

asked Jul 19 '17 at 10:44

Jennifer

Please update your question defining what $v_i$, $u_i$, and $A$ are? – unseen_rider Jul 19 '17 at 18:42
@unseen_rider, I have updated my question as above. – Jennifer Jul 25 '17 at 05:51
Ok I presume $A$ is the Area of the whole cross section? – unseen_rider Jul 26 '17 at 16:47

How to integrate ∫vᵢ(uᵢ² + vᵢ²)dA in calculating monosymmetry index of an angle?

0 Answers0