3

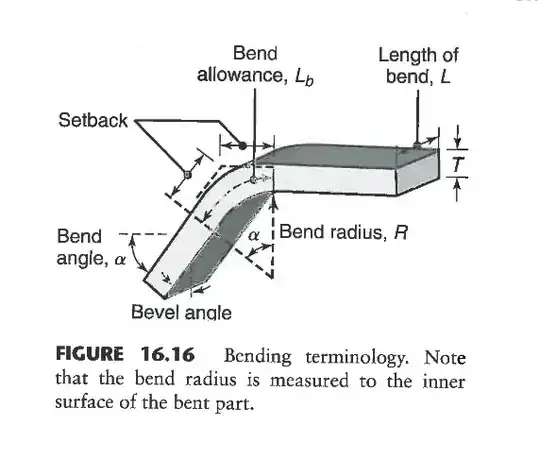
I'm used to calculate the minimum radius required for bending operations on both aluminum and steel sheets, given the following parameters: https://imgur.com/a/7akHC

Problem statement:

For a sheet metal stock with inch thickness, determine the minimum tool radius for both the steel and aluminum alloys that will not tear the material. Assume the sheet of material is in pure bending (i.e., no additional tension is applied during forming).

I have already learned about the following formulas:

  • R = 1/k
  • k(y) = e(y) / (h/2)
  • e(y) = k.y

Given that R = 1/k, the next step is to find the maximum curvature k for each sheet.

The problem is that I don't know how to find the maximum curvature, and I'm still stuck.

Any thoughts?

do-the-thing-please
  • 4,011
  • 1
  • 15
  • 29
user6039980
  • 151
  • 1
  • 9
  • 1
    Is there an error in your equations? Does R depend on little k, or big K? What are y and h? My guess is that y is distance from neutral plane and h is total wall thickness. If I have this all correct in my head, your equations are monotonic in all the variables, so there is no maximum. Are you perhaps missing a constraining equation that relates radius to stress in the material? – do-the-thing-please Nov 06 '17 at 18:04
  • 1
    @starrise There is no big K, sorry but I meant 'k' the curvature. y = distance from the neutral axis to the top of the sheet cross-section. h = thickness of the sheet. – user6039980 Nov 06 '17 at 21:03
  • 1
    @starrise "Are you perhaps missing a constraining equation that relates radius to stress in the material?" - There is no constraining equation specific to the problem. But I'm pretty sure that there is a solution for finding the minimalist radius. – user6039980 Nov 06 '17 at 21:28
  • 1
    @starrise I updated the question in order to provide more information about the problem, please check it out. – user6039980 Nov 06 '17 at 21:42
  • 2
    Thanks for the update. I think that there is a constraint, but based on the answer from Derkooh it is empirically derived. I suppose what I was getting at is that the tighter the radius, the greater the plastic strain. If the strain exceeds the failure strain the material ruptures. So stress/strain must be related to this in some way. – do-the-thing-please Nov 06 '17 at 22:36

1 Answers1

3

I hope the following helps. This is from a book I used in college. Manufacturing Engineering and Technology, 5th Ed. by Kalpakjian and Schmid

enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

Minimum Bend Radius

Where **r** is the tensile reduction of area.

enter image description here

Todd Takala
  • 337
  • 2
  • 19
  • 1
    Thanks a lot for sharing - that book seems interesting. If I understand correctly, the minimalist radius can be obtained by `Rmin = 1 / ((2/(h.k)) + 1)`? – user6039980 Nov 06 '17 at 23:20
  • 2
    I highlighted the min bend radius equation – Todd Takala Nov 06 '17 at 23:23
  • 1
    Perfect. What is `r`, then? – user6039980 Nov 06 '17 at 23:27
  • 2
    `r` is tensile reduction of area, and is approximated through the chart in Fig. 16.18.. I also added Fig 16.16 to the derivation. – Todd Takala Nov 07 '17 at 01:07
  • 1
    I'm sorry, but I'm unable to determine it from the figure. Also how can I obtain it? – user6039980 Nov 07 '17 at 01:50
  • 2
    R/T is the y-axis, and r (tensile reduction of area) is the x-axis. – Todd Takala Nov 07 '17 at 01:55
  • 2
    `R/T` is the y-axis, and `r` (tensile reduction of area) is the x-axis. Minimum bend radius `R` is a function of material thickness and material, and is empirically defined from table 16.3. Eq. 16.5 can be solved for `r` as follows: `r = 50 / (R/T +1) ` – Todd Takala Nov 07 '17 at 02:02
  • 3
    Still available on Amazon : a good investment? https://www.amazon.ca/s/ref=nb_sb_noss?url=search-alias%3Daps&field-keywords=Manufacturing+Engineering+and+Technology – Solar Mike Nov 07 '17 at 06:42
  • 1
    @Derkooh OK. Your answer is informative, but it hasn't yet provided a solution for the problem, given the params provided at https://imgur.com/a/7akHC. Could you please provide a solution for the calculus of the Rmin of both steel and aluminum sheets? – user6039980 Nov 07 '17 at 11:39
  • 1
    @SolarMike Yeah, for sure. – user6039980 Nov 07 '17 at 11:40
  • 1
    @Kais Derkooh says at the top of his answer "I hope the following helps" so it's now down to you to apply the information... – Solar Mike Nov 07 '17 at 11:53
  • 1
    @Kais R =6T from table 16.5 if you assume the material is hard aluminum. No calculus is needed. Chart 16.18 is empirically defined for multiple materials. – Todd Takala Nov 07 '17 at 13:04
  • 1
    @Derkooh Ok, understood. – user6039980 Nov 07 '17 at 16:33