Deriving the amplitude of a coulomb (dry friction) damped spring

Question

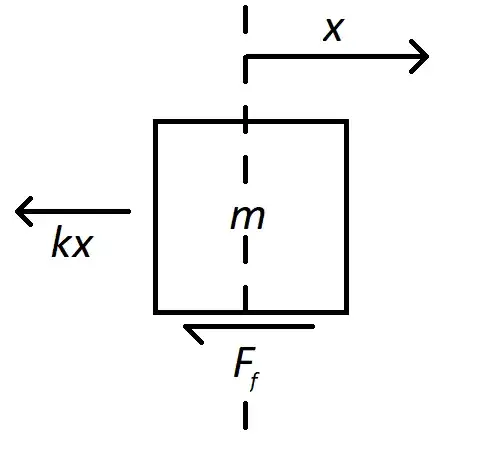
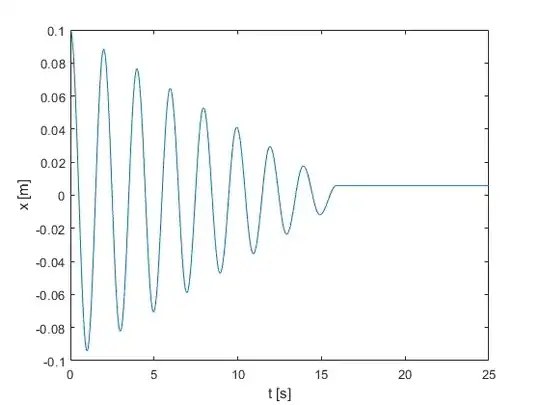
This is my first time posting anything, but I could not figure out the derivation of the amplitude of the spring for the 4 first oscillations. I am not acquainted with the effect and calculations of damping since I am only in high school. This is an assignment I have, I think I am in over my head, but I have invested too much time in this to change the topic. I figure that the only deviation to the classic coulomb damping where the source of energy dissipation is due to the weight sliding on top of a surface, and the force of friction is constant and does not change, is that the friction coefficient changes as more coils enter the paper cylinder which is compressing the spring. The values that I have is the frictional force of when the entire spring is within the paper cylinder, the mass of the weight, the initial elongation of the spring (x naught) and the spring constant. 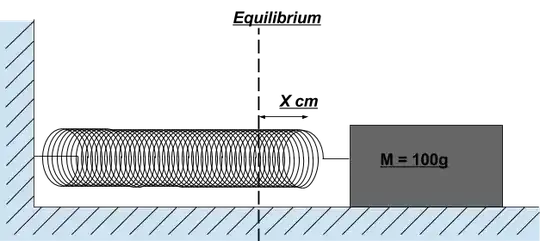. If anyone can help me with my assignment I would be eternally thankful! If not, I would gladly take any help with deriving the amplitude of the classic coulomb damping case as seen above as a backup. Moreover, If there is any rule that I am breaking with this post, let me know. This is as previously stated, the first time that I post anything, and it is due to pure desperation as I am way in over my head! Thanks in advance!

I got 15 experimental values for the amplitudes at half revolution increments for 4 revolutions, took the averages and inserted them into a graph. The graph can be seen here: https://gyazo.com/3e2d1c18b05a31d1eca88c411bdbb2cb .

To solve the equation for x(t) in the equation ma = -kz +F_r, where you would get Asin(wt) + Bcos(wt) + F_r/k, you merely need to equate it to the initial displacement to calculate B, and equate it to the derivative of displacement i.e. initial velocity to get A. A is zero if there is no initial velocity, but the question still stands, how do you get -sgn(v) so that it can be used as the value of friction over spring constant which would give the damping term. I suppose it could be gotten by taking -v/magnitude of v, but how would you calculate the magnitude of v? Since solving the equation without it would merely result in a regular cosine function.

Answer 1

As this is for school, I don't want to just give you the answer. I will do my best to give you some direction without completely giving it away. Don't feel bad that you are feeling desperate, these are the problems where you learn the most. Do not give up and stay persistent. Your ability to understand has nothing to do with being in high school but with your dedication to learning.

Spring displacement is purely a function of force and displacement. in this case you should not just consider the static forces acting on the spring but also the d'lambert force (dynamic) force. Recall that F=Ma. do your free body diagram but also consider the dynamic force in your FBD (which opposes changes in direction) for your derivation, start with the equation of motion.

x(t) = a0+a(t)^2 + v0+v(t)*t + x0. where a0, v0 and x0 are the values of acceleration, velocity and position at time=0 which you know.

Your dynamic load will be mass X the acceleration term in the equation of motion. you can solve for the acceleration component by rearranging the equation above. to get the force, multiply both side by the mass. you can then plug and chug in excel to get the answer(0

the effect of friction will depend on velocity. you can google to learn more about damping coefficients and its time dependent nature.

Answer 2

If by dry friction you mean a force that is constant with respect to velocity and points in a direction opposite to the velocity, then finding a closed form solution to your problem will be extremely challenging. It will depend very much on the actual form of the damping force function and I'd wager it would be impossible in most cases.

Checking Wikipedia, this is indeed your case, as Coulomb damping is given by the combination of static and dynamic friction as seen here, the relevant equations are $$ \begin{aligned} F_f\leq \mu_sN\qquad \text{if }v=0 \\ F_f=\mu_dN\qquad \text{if }v\neq0 \end{aligned} $$ where $\mu_s$ and $\mu_d$ are the static and dynamic friction coefficients.

To derive the equation of motion, first construct a free body diagram like the following

Note that the spring force always has opposite sign to the displacement $x$ and the friction $F_f$ always points opposite to either the velocity (when $\vert v \vert>0$) or the spring force (when $\vert v \vert=0$).

So, writing $ma=\sum F$ nets you $$ m \ddot{x}=-F_f(\dot{x},x)-kx $$ leading to your equation of motion being $$ m \ddot{x}+F_f(\dot{x},x)+kx=0 $$ Notice that the frictional force $F_f$ is a function of both position and velocity. (Check the Wikipedia article I linked)

Your best bet for a non-linear problem like this is numerical simulation. Here's a quick and dirty numerical simulation in MATLAB using Forward Euler's method (I won't show how to transform the second order ODE to first order, but if you are interested, leave a comment)

clear variables
close all
clc

%Input parameters
m=0.1;                %Block mass [kg]
k=1;                %Spring stifness [N]
mu_s=0.008;         %Static dry friction coefficient, Fr<= mu_s*N when body is at rest [#]
mu_d=0.003;        %Dynamic dry friction coefficient, Fr= mu_d*N when body is in motion [#]
x0=0.1;             %Initial displacement [m]
v0=0.0;             %initial velocity [m/s]
T=25;               %Total simulation time [s]
dt=0.00001;         %Approximate simulation timestep, gets rounded to make number of time steps an integer [s]

%Calculations
g=9.806;            %Acceleration of gravity [m/s2]
n=ceil(T/dt)+1;     %Number of timesteps
t=linspace(0,T,n)'; %Time vector

x=zeros(size(t));   %Solution vector for position
v=zeros(size(t));   %Solution vector for velocity

x(1)=x0;            %Initial conditions
v(1)=v0;            %Initial conditions

for i=2:length(t)   %Solution loop
    x(i)=x(i-1)+dt*v(i-1);
    v(i)=v(i-1)+dt*(-1/m*fr(x(i-1),v(i-1),m,g,k,mu_s,mu_d)-k/m*x(i-1));
end

plot(t,x)
xlabel('t [s]')
ylabel('x [m]')   

%Coulomb friction, velocity is considered to be zero below a threshold
function f=fr(x,v,m,g,k,mu_s,mu_d)
    if abs(v)>1e-6
        f=mu_d*m*g*sign(v);
    else
        f=-min(mu_s*m*g,abs(k*x))*sign(x);
    end
end

The following is the solution for the parameters in the code

An interesting phenomena we can catch is that, if the static friction coefficient is sufficiently big, the spring cannot overcome the frictional force, leading to the block "remaining stuck", which is intuitive enough. Setting $\mu_s$ to $2$ leads to the following solution.

Intuition confirmed :)

Let me know if you have any questions.