Beams question help

Question

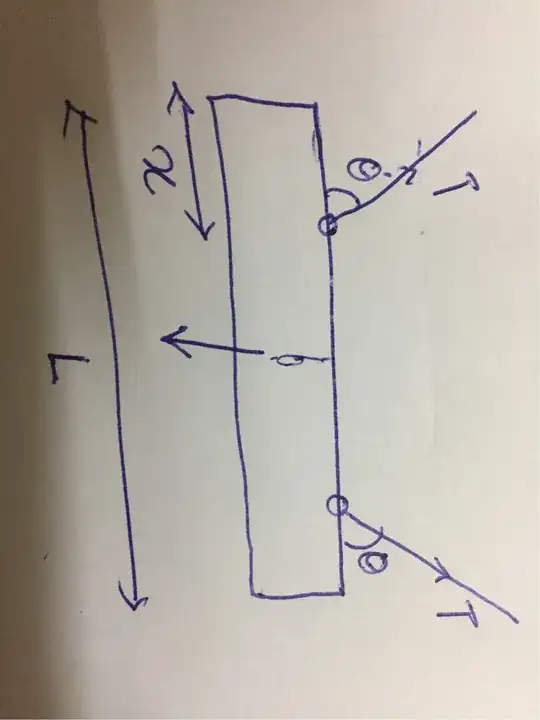
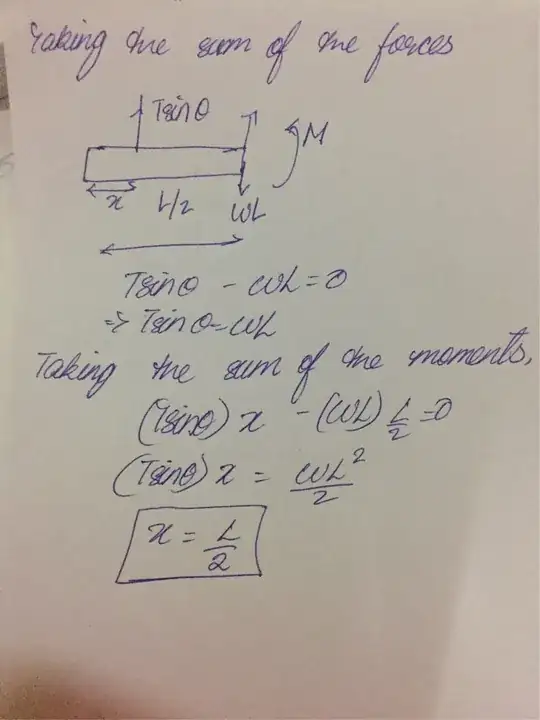
I tried to solve this question I arrived at this diagram but taking the moments about the center of the beam I arrived at x=L/2. Can someone tell me what I need to do to get the correct answer?

Answer 1

Second Attempt:

After reading your comments, I approached the problem using a different process.

Step 1: Find the y-forces using $\Sigma$$F_y = 0$.

$(2\cdot Tsin(\theta))$ - $(W\cdot L)$ $=0$

$2Tsin(\theta)$ = $WL$

Step 2: Treat the beam as a collection of beams.

I decided to break the beam into three parts. The outside edges can be thought of as cantilever beams that are attached by the supports.

Step 3: Making the first cut at the midpoint to the left support.

Using the formula for bending moment of a simple beam under a uniformly distributed load, we can determine that $M_{mid} = \frac{WS^2}{8}$

Step 4: Making the second cut at the left sling.

Using the formula for bending moment of a cantilever beam under a uniformly distributed load, we can determine that $M_{cantilever} = \frac{Wx^2}{2}$

Step 5: Setting equations equal and solving.

From left end, to get the sum of moments to equal zero, $M_{cantilever} = \frac{M_{mid}}{2}$

Therefore:

$\frac{WS^2}{16} =\frac{Wx^2}{2}$

$WS^2=8Wx^2$

$S^2=8x^2$

$S = 2\sqrt{2}x$

Final:

As you can see, the center span $S = 2\sqrt{2}x$. Because $S = L-2x$, you can substitute to find the equation $L-2x = 2\sqrt{2}x$

$L = 2\sqrt{2}x + 2x$

$L \approx 4.8284x$

$x \approx \frac{1}{4.8284L} \approx 0.2071L$

_

Where $x$ is the distance from a support on the beam to the left end of the beam.

Where $S$ is the span of the beam.

Where $L$ is the length of the beam.

To clarify, the beam of length $L$ is divided into three sections; the left cantilever of length $x$, the center span $S$ of length $L-2x$, and the right cantilever of length $x$.

Where $Tsin(\theta)$ is y-component of the tension force.

Where $W$ is the weight of the beam.