Skewing of joints using virtual work

Question

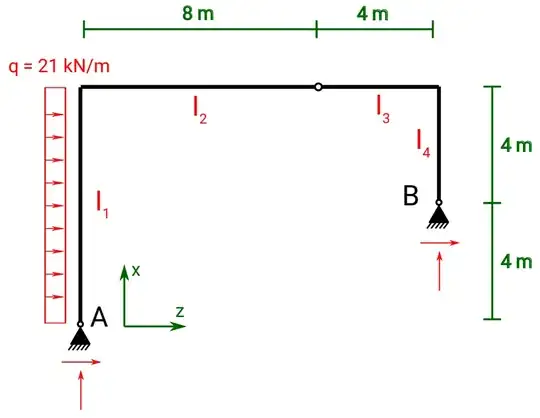
Given ist the following framework:

$$E=210 \frac{\text{kN}}{\text{mm}^2}$$ $$ EA \to \infty $$ $$ I_1 = 80000\text{cm}^4 $$ $$ \frac{I_1}{I_2} = \frac{3}{4} $$ $$ I_3=I_1 $$

Using the principle of virtual work, I'm suppossed to figure out by what angle $\varphi_i$ beam 2 and 3 are skewed. Shear forces can be omitted.

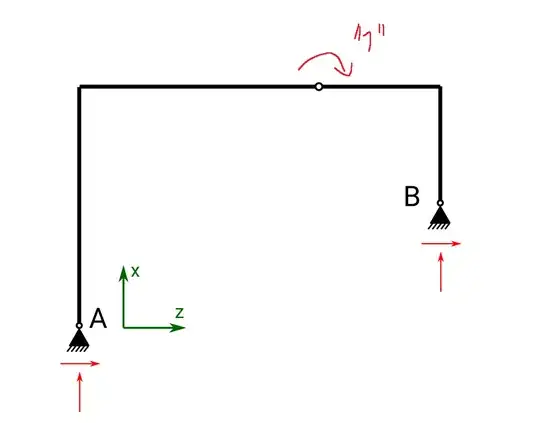
In my virtual system, I apply a moment at the joint:

How can I determine the reaction forces needed in my virtual system? I assume that the moments in 1 and 4 need to be 0, but there is no way to cancel out the moments at the ends of 2 and 3 and still have a force equilibrium.

Or is my understanding of a balanced virtual system flawed?

Any help is greatly appreciated. Thanks!

In case someone wants to work through the problem themselves, here is the solution and what I've calculated so far:

Solution: $$\begin{align*} \varphi_2&=0.009\text{rad}\\ \varphi_3&=0.007\text{rad} \end{align*}$$

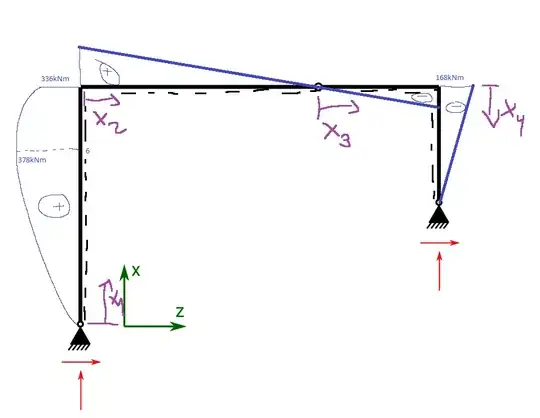
Calculation:

$$EI_1 =EI_3= 210\cdot 80000\cdot 10^4\text{kNmm}^4=168\cdot 10^9\text{kNmm}^4 = 168\cdot 10^3\text{kNm}^4$$ $$ EI_2=\frac{4}{3}EI_1=224\cdot 10^3 \text{kNm}^4$$ Reaction Forces: $$ \begin{align*} A_x &= -126\text{kN}\\ A_y&=-42\text{kN}\\ B_x&=-42\text{kN}\\ B_y&=\hphantom{-}\text{42kN}\\ G_x&=\hphantom{-}42\text{kN}\\ G_y&=-42\text{kN} \end{align*} $$

Since we ignore shear forces and $EA\to \infty$ we only need to consider moments.

The moments can be calculated to: $$\begin{align*} 1:&-q\frac{x^2}{2}+126x=-\frac{21}{2}x^2+126x\\ 2:&-42x+336\\ 3:& -42x\\ 4:& 42x-168 \end{align*}$$

Answer 1

Let's assume that in equilibrium the links 1 and 4 will be at angles $\theta_1$ and $\theta_4$ with the vertical.

The relationship between these angles can be determined from the fact that the horizontal length between points A and B is $8+4=12$.

$$ 8 \sin \theta _1+8 \cos \theta _1+4 \sin \theta _4+4 \cos \theta _4 =12 \ \ \ (1)$$

The external forces acting on the links are their masses $m_i$ and $q$. The masses can be determined from the inertias. (The question does not make clear about what point the inertias are calculated, and also the units seem wrong. So I will just leave the equations I terms of the masses.)

The virtual work by $q$ can be calculated as $$ \delta W_q=\int _0^8q \ \delta (l \ \sin (\theta_1 ))dl = 32 q \cos \theta_1 \delta \theta_1=672000 \cos \theta_1 \delta \theta_1 $$

The virtual work due to masses:

$$ \delta W_1= m_1 g\ (-\delta(4 \cos \theta_1))= 4 m_1 g \sin\theta_1 \delta \theta_1$$

$$ \delta W_2= m_2 g (-\delta(8 \cos \theta_1-4 \sin \theta_1)))=m_2 g (8 \sin \theta_1+4 \cos \theta_1)\delta\theta_1$$

$$ \delta W_3= m_3 g\ (-\delta(2 \cos \theta_1))= 2 m_2 g \sin\theta_4 \delta \theta_4$$

$$ \delta W_4= m_4 g (-\delta(4 \cos \theta_4-2 \sin \theta_4)))=m_2 g (4 \sin \theta_4+2 \cos \theta_4)\delta\theta_4$$

From $(1)$ we have $$ 8 \cos \theta_1 \delta\theta_1-8 \sin \theta_1 \delta\theta_1+4 \cos \theta_4 \delta\theta_4-4 \sin \theta_4 \delta\theta_4=0$$

which can be solved for $\delta\theta_4$ in terms of $\delta\theta_1$.

If we sum all the virtual works and set them to zero, and substitute for $\delta\theta_4$ in terms of $\delta\theta_1$ we get the second equation.

$$ \delta W_q+\delta W_1+\delta W_2+\delta W_3+\delta W_4=0 \ \ \ (2)$$

The two equations $(1)$ and $(2)$ have two unknowns $\theta_1$ and $\theta_4$ which must be solved with the values of $m_i$ and $g$.