How cold for lack of heat?

Question

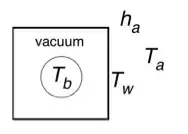
I know that on the moon, while the daytime surface temperature can be above 270° F, in the shade but a few feet above the surface temperature can get quite low. Wondering whether a similar phenomenon can be observed if a vaccum is created around an object which is suspended in he middle of it.

Say for example, a steel ball is suspended in the middle of a plexiglass cube, by 3 plexiglass threads, and the interior volume of the cube is 1 cubic meter, and the ball has a diameter of 10cm, the box walls are 5cm thick. The cube has been evacuated to the practical limit of modern vacuum pumps. Let's say the steel ball is chilled to a temperature of -20 c (measured at the time the evacuation is complete). Let's say it's 70° F outside, and the box is sitting on a plexiglass tripod in the shade, shielded from direct sunlight.

What would be the temperature reading of the steel ball, approximately, after say 2 weeks? (i.e. at equilibrium).

(I don't mean to be overly prescriptive, but trying to be sufficiently specific to avoid answers like "it depends on how thick the walls are" and similar)

Regarding your first question, remember the atmosphere of earth absorbs energy as well, the amount of energy your system would receive on the earth is not same as it would receive on the moon. And i don't understand how 'The box' comes into play ? It's not quite clear to me. — Sam Farjamirad, Aug 19 '18 at 17:32
the purpose of the box is to create the vacuum around the steel ball, to insulate, as much as reasonably possible the steel ball from the radiant heat of the earth and the surrounding atmosphere, just as on the moon, the lack of atmosphere insulates something above the surface from the very high temperatures on the surface. i.e. the heat can't travel from the wall of the box to the steel ball because there is no medium to conduct it. That's the question anyway. — GGizmos, Aug 19 '18 at 17:36
I think i got it, so you want to reduce the heat transfer by conduction and convection as much as it is possible, but you forget the transfer heat by radiation. I think your thermodynamic system would be in equilibrium in two weeks. — Sam Farjamirad, Aug 19 '18 at 17:40
Ah. Does heating by radiation require a medium of any kind? if you remove the difference between the earth and moon, i.e. an atmosphere, why the behavior seems to be different (or perhaps not?). If the box were shielded from visible light, infrared ultraviolet would radiant heating still occur? how does this happen? — GGizmos, Aug 19 '18 at 17:49
Heat radiation is an electromagnetic radiation, so it doesn't require any medium. The heat radiation continues if you isolate the system from the sunlight, a good example is the sun, if we neglect the effect of interstellar radiation, nothing warms the sun up from outside, it keeps radiating its energy units it rans out of fuel, your steel ball would radiate its energy until its temperature reaches -273.15 °C. — Sam Farjamirad, Aug 19 '18 at 17:55
According to wikipedia, radiation of heat mainly happens by infrared waves. Certain materials, aluminim foil for example, reflect most of the infrared that strikes it (95% apparently). If you covered this box with aluminimu foil would you expect equailibrium effect to take ~20x longer? — GGizmos, Aug 19 '18 at 17:58
Prior the electromagnetic waves hit the aluminium, they reach the box, and plexiglas cube, and after reflection of the waves they reach the box and the cube again, you your steel ball receive few reflected energy back. But the box and cube re-emit the heat waves but in all directions, again the ball receives a fraction, the better way is to cover the ball with aluminum foil instead of the box. — Sam Farjamirad, Aug 19 '18 at 18:18
Good idea, but if the aluminum foil covers the box, not sure why you say "prior the electromagnetic waves hit the aluminum they reach the box." No matter though I get the point. — GGizmos, Aug 19 '18 at 18:23
"Does heating by radiation require a medium of any kind?" No. If it did require a medium, you wouldn't feel any heat coming from the sun! — alephzero, Aug 19 '18 at 19:48
Making the setup more complicated with aluminium foil etc won't make much difference. The foil will emit heat radiation, just like everything else which is not at absolute zero temperature. And if the foil reflects 95% of the radiation that falls on it, then 95% of the radiation from the ball inside will be *reflected back onto the ball* and re-absorbed by the ball. The foil might stop radiation getting to the ball from outside, but it also stops the *ball* radiating heat away and keeps it warmer than if the foil was not there at all. — alephzero, Aug 19 '18 at 20:00
Everything tends to the same temperature over time - give enough tme... — Solar Mike, Aug 20 '18 at 05:51

Jeffrey J Weimer · Accepted Answer · 2018-08-20T21:50:16.263

Imagine the system below at equilibrium.

The energy balances are as follows:

At the ball ...

$$\epsilon_b T_b^4 =\epsilon_w T_w^4$$

At the wall ...

$$\epsilon_w A_w \sigma T_w^4 = h_a A_w (T_a - T_w) + \epsilon_a A_w \sigma T_a^4$$

In these balances, $\epsilon_j$ are emissivities, $A_j$ are areas, $\sigma$ is the Stefan-Boltzmann constant, $T_j$ are temperatures, and $h_a$ is the convection coefficient of air.

Choose all materials and sizes to specify all $A_j$ and $\epsilon_j$ values. Choose a still or windy day to specify $h_a$. Define the air temperature. This leaves two unknowns ($T_b$ and $T_w$) with two equations. The problem can be solved.

Example

Take the case where the ball and walls are the same material so their emissivities are the same. We find that $T_b = T_w$. The radiation heat flows inside the box are balanced. Now assume the air has no radiation and the walls are perfect black bodies ($\epsilon_w = 1$) to obtain $\sigma T_w^4 = h_a (T_a - T_w)$. Take stagnate air with $h_a = 5$ W/m$^2$ K and $T_a = 275$ K. The wall and ball are at 238 K. In this case, the air is pumping heat to the walls by convection, and the (black body) walls are radiating back to the air. As the walls (and ball) go toward gray bodies (as $\epsilon_w \rightarrow 0$), the wall temperature increases. In the limit where the walls emit no radiation, we end with the simple case that $T_b = T_w = T_a$. No heat flows from anything at equilibrium.

Thanks that's very helpful Jeffrey. I'm afraid I don't quite what the units and some of the letters are. (e.g. Aw, e, sigma?) Assuming no wind, can you give an example based on the setup described above? — GGizmos, Aug 20 '18 at 16:55

How cold for lack of heat?

1 Answers1

Example