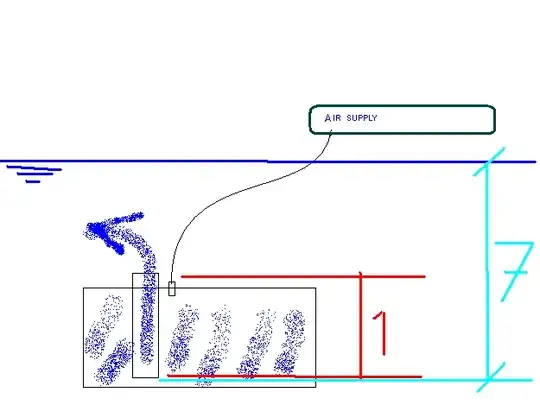
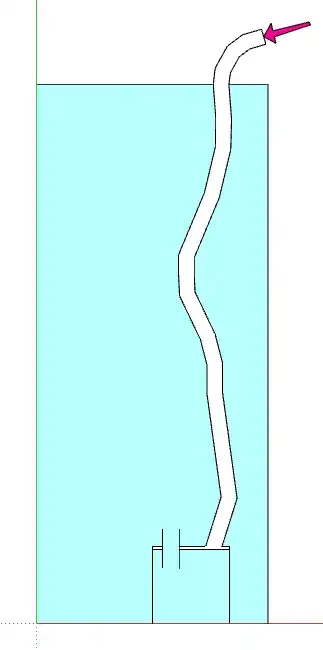
How much pressure would I need or, better yet, how do I compute for the pressure required to push water out of a submerged tank? Do I use 1 meter as head or 7 meters? (Please just bear with the drawing :) )
-
Is the tank underwater? What is going to hold it down as the water is replaced with air? Or is that the objective? – Mark Aug 30 '18 at 04:13
2 Answers
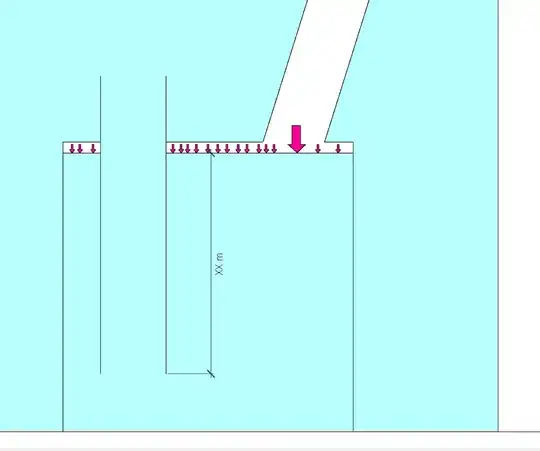
Taking a look at the tank initially:
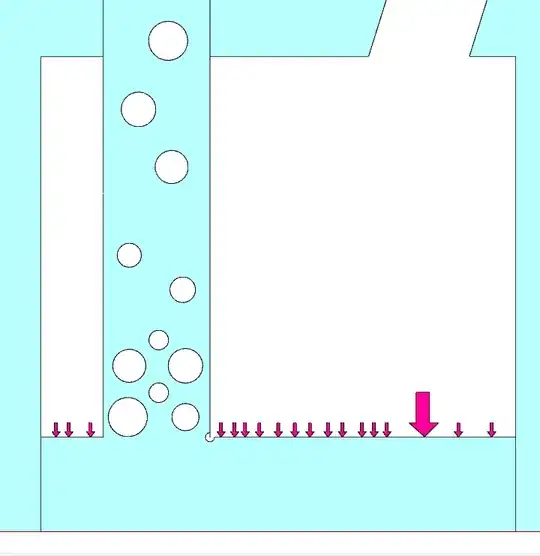
We have pressure at the top, and with air you've got about the same pressure. Zooming in on the bottom, the picture is pretty clear.
To hold this position, the sum of forces must be equal:
$$ P_{air}A_{tank} = P_{liquid}A_{liquid} $$
Since the area the air is pushing on is the same as the area the water is pushing on the air, the pressures are equal. In this position, the pressure of the air must have the same head as the liquid, or 6 meters.
We look into this second position. Note this is the most the air can push out the liquid. If the liquid level was lowered, the air would bubble out the tailpipe. In this picture, the pressure of the air must be equal to 6 meters plus the height of the tailpipe, XX meters. In the limit where the tail pipe reaches the bottom, the pressure would be equal to 7 meters.
- 5,333
- 13
- 47
-
I deleted my answer, but I note that you have not included any losses... no pumping losses then? – Solar Mike Aug 30 '18 at 16:04
-
@Solar Mike I did static as I interpreted the question as "minimum", as a desired flow rate wasn't given. The dynamic always needs friction losses, but that requires extra information that we don't have. – Mark Aug 30 '18 at 16:06
-
that is why I included the term losses in my answer, even though any info about time / rate etc was not given. – Solar Mike Aug 30 '18 at 16:08
-
@SolarMike - It's definitely important, and I was commenting for an expansion of the answer. Discussing things such as what would be needed to calculate those losses (such as friction factor equations on the air line, and friction factor equations on the water line, presuming a small nominal loss for the flow of liquid in the tank, and entry and exit losses of both air and water), would have made a great answer. – Mark Aug 30 '18 at 16:14
-
You did not ask or suggest an expansion - you just said " it's not very helpful" - comments suggesting improvements actually suggest them... – Solar Mike Aug 30 '18 at 16:20
-
@SolarMike - Sorry. I'm a bit of a terrible communicator. You are correct it would have been better with that. – Mark Aug 30 '18 at 16:24
you need to supply no head pressure.
The reason is as per your diagram the tank and its drain duct are connected at the open bottom. The pressure is equal on the drain duct to that of the tank and equal to the water it is submerged into at all levels and all locations.
So given enough time the lake water will replace the tank's water. Any small pressure in the hose will expedite this process. if you want the pressure at the discharge of the hose is 6 meters.
- 21,714
- 2
- 18
- 38
-
1
-
@JonathanRSwift, it is not possible to fill this tank with air, it will bubble up from the open duct and water will rush in. – kamran Aug 30 '18 at 13:41
-
@kamran - I have a different interpretation on the "drawing", but I see where you are going. Perhaps a drawing of your own to explain the matter for our new member would be helpful. – Mark Aug 30 '18 at 15:12
-
1@kamran - I have a different interpretation on the "drawing", but I see where you are going. Perhaps a drawing of your own to explain the matter for our new member would be helpful. Like the silly math problem of 6/2(1+2) which is really just an annotation problem, this seems like something that just has different answers depending upon communication. – Mark Aug 30 '18 at 15:59
-
@kamran The drawing seems to show the duct coming through to the bottom of the tank, while the air is coming in at the top. It can't get down low enough to bubble out until the rest of it is filled with water. – JMac Aug 30 '18 at 16:03
-
My answer refers to Blaise Pascal law of communicating vessels. What i meant by water of the pool replacing the water in the tank is either by micro currents or by turbulence or by convection the waters that have identical hydrostatic pressure will mix and there is no need for pumping. – kamran Aug 30 '18 at 20:12
-
The question was about the _air pressure_ required to pump the tank water out of the tank, and keep the water from coming back in. It's really not clear from the answer and comments how this relates to that. – JMac Sep 24 '18 at 14:34