As an example, consider a P-T1-system with a PID-controller. First look only at the P-T1 system, set a $y_r$ and wait a long time - then we take a look on its output $x$ and see that it has still a disturbance $d$ which variates with time (see the plot, system output $= x$). In this model, the system output is, after you wait a long time, a constant plus $d(t)$.
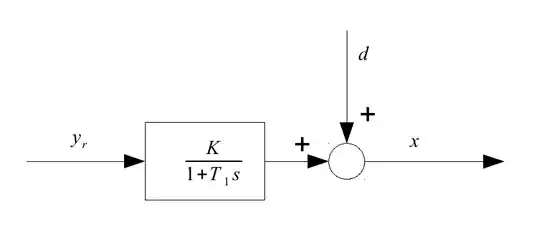

The next step is to introduce a PID-controller:
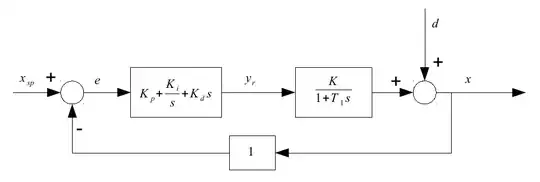
For this loop alone we could just use some experience-based technique like the Ziegler and Nichols procedure to adjust its parameters $K_p$, $K_i$ and $K_d$ optimally. If we switch to discrete control loop, because the controller is digital, we will have one additional parameter: The $\Delta t$ at which the controller operates.
What $\Delta t$ is required for the control loop to diminish the effects of $d$ on the system output? The trend will of course be the smaller $\Delta t$ the better, but is there a general rule for the maximum $\Delta t$?