11

I have built (several) discrete Extended Kalman Filters (EKF). The system model I am building has 9 states, and 10 observations. I see that most of the states converge except one. All except 1-2 of the EKF state estimate appears to drift. Since the EKF is dependent on all the states being convergent, the rest of the states are very erroneous after the divergence.

How do I check the observability of the EKF? Do I simply check the rank of the measurement Jacobian and see if it's less than the maximum rank of the measurement Jacobian?

After adding more measurements in my simulation, I was able to get things to converge. However, my question about observability still remains!

Issue:

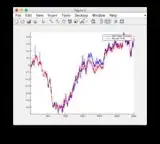
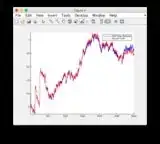
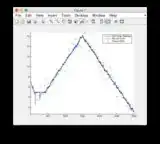
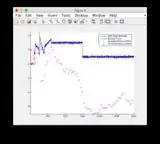
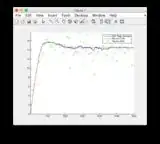
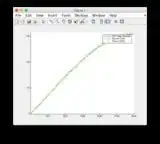
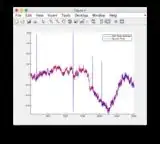
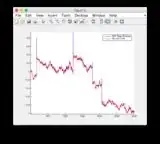
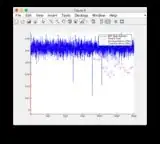
Ground truth and EKF estimate graphs can be found here or see below.

Notes:

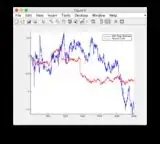
  • The model is quite non-linear between time steps 400-600 hence some divergence of some of the states
  • Figure/State 6 is the one that seems to be diverging
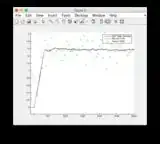
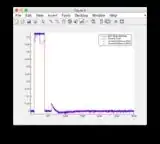
  • Please ignore the "sensor readings" plots for Figures 8/9

Things I have tried:

  • I know for linear state space systems you can use the Cayley Hamilton Theorem to check observability.
  • I have tried to check the Innovation/measurement residual e and all innovations converge to 0
  • I've also tested different inputs and they don't seem to affect the convergence of the diverging state(s)
  • I've tuned the EKF without any sign of convergence for the diverging state(s)
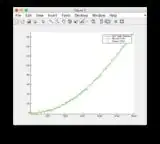
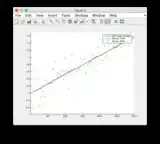
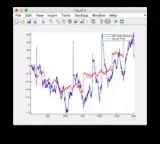
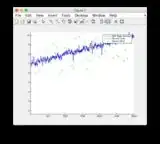
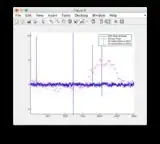
  • Graphs for another input signal: or see below
  • After talking to a colleague, he suggested that I investigate another issue that could be that there is an observation that is linearly dependent on 2 states, e.g. y = x1 + x2. There is an infinite number of values that could satisfy the same y, but shouldn't observability capture this issue as well?

Please let me know if there's anything else I can provide.

Ground truth & EKF estimate graphs:
Click on image for larger view

image a image b image c image d image e image f image g image h image i

Additional input signal:
Click on image for larger view

image m image n image o image p image q image r image s image t image u

Rodrigo de Azevedo
  • 247
  • 1
  • 8
krisdestruction
  • 211
  • 1
  • 7
  • I see that this site references `rank(O) = [H; HA...] = n`. The only issue is that I have something like `sin( x(3) )` or sine of state 3. Do I linearize it to `x(3)` and treat it as part of the A matrix? I'll take a shot at this in the morning and report back. https://cwrucutter.wordpress.com/2012/11/12/observability-of-gps-measurements-in-an-extended-kalman-filter/ – krisdestruction Apr 21 '15 at 08:01
  • @ChrisMuller yeah I thought of embedding the images to the question, but I don't think it works with multiple images (albums). Thanks for the tag update. I checked the link above and I don't know if I should be linearizing it. – krisdestruction Apr 21 '15 at 17:59
  • 1
    I'm pretty sure it doesn't. You could do it by making a gif, but it might be a big headache depending on how you originally generated the plots. – Chris Mueller Apr 21 '15 at 18:02
  • @ChrisMueller All from Matlab, I simply took screenshots of the graphs in OS X. – krisdestruction Apr 21 '15 at 18:02
  • 1
    It's possible to bring the images inline, but it takes a little bit of work. I have edited to separate the images out of the imgur link and I have set the images so you can click through and see the larger image. –  Apr 23 '15 at 13:41
  • Would a feature request on the meta would be a good idea? – krisdestruction Apr 23 '15 at 16:46
  • Unless it's already built into markdown of course. I don't understand the new code to generate the images in the question but whatever you did, I like it! – krisdestruction Apr 23 '15 at 17:30

1 Answers1

1

Using this reference on linear discrete Kalman Filters, it looks like you can apply a standard observability model. Namely, for a linear Kalman Filter system defined as

$$ \begin{align*} x_{k+1} &= A x_k + B u_k \\ y_k &= C x_k + D u_k, \end{align*} $$

the system is observable if $M_{obs}$ is full rank, where $M_{obs}$ is defined as:

$$ M_{obs} = \begin{bmatrix} C \\ C A \\ \vdots \\ C A^{n-1} \end{bmatrix} $$

and

$$ \begin{bmatrix} C \\ C A \\ \vdots \\ C A^{n-1} \end{bmatrix} x_0 = \begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_{n-1} \end{bmatrix}. $$

An EKF is just a linear Kalman Filter with Jacobians substituded in for $A$, $B$, $C$, $D$. By using an EKF, I assume that your state kinematics are adequately linearizeable, so observability for EKF should follow the same formulation as above.

deeroh
  • 11
  • 2