How can I calculate the amount of heat my copper water trap can dissipate?

Question

My small (1.5hp) air compressor is connected to a water trap made of 8mm copper of about 4 metres length. The idea is that you push the compressed air through the piping which cools it, condensing the water out (which you drain away) and thus sending dry air to your air tools.

I know the system works, but i would like to understand the maths behind it. I started trying to work it out with help of the below graph from engineeringtoolbox.com but didn't know where to go next.

How can I mathematically determine the temperature drop of the air in the piping? We can assume an average ambient temperature of 25 degrees Celcius with air coming out of the compressor at 100 degrees Celcius.

Answer 1

A poor method to remove water. The air velocity from a relatively large compressor into a small line will atomize the condensed water and give a "fog" at discharge. Why not use the standard efficient system ? Normally the compressor discharges into a large ( steel ) tank where the water condenses to the bottom and is periodically drained. My 1/3 Hp compressor used a very short length of about 12 mm tubing into the reservoir , so your 8mm tubing on a 1.5 Hp compressor will result in very high velocities when flowing. The standard reservoir system worked fine for condensate control when I used it to paint a couple cars.

Answer 2

$$ T_{out} = \frac{\dot{Q}}{\dot{m}C_p}+T_{in}$$ Where T is temperature, $\dot{Q}$ is heat rate, $\dot{m}$ is mass flowrate and $C_p$ is the specific heat of air at constant pressure. To check the units: $$T_{out}[C] = \frac{\dot{Q} \left[\frac{J}{s}\right]}{\dot{m}\left[\frac{kg}{s}\right]C_p\left[\frac{J}{kgC}\right]} + T_{in} [C]$$ To clarify, $\frac{J}{s} = W$, and these are SI units (Joule, kilogram, Celsius).

Answer 3

Pipe (Dry) Air Flow

Theory

Start from the air flow through the pipe. The energy balance equation below considers only convection from the outer air and takes a lumped analysis of the fluid in the pipe. In this, P is the perimeter length of the pipe.

$$ \dot{m}\tilde{C}_p\frac{dT}{dx} = - h_a P (T - T_a) $$

Given the tube length $L$ and the entering hot temperature $T_h$, we recast this as a dimensionless expression using $\Theta = (T - T_a)/(T_h - T_a)$ and $X = x/L$.

$$ \frac{d\Theta}{dX} = -\beta \Theta $$

The dimensionless factor $\beta = h_a P L / \dot{m}\tilde{C}_p$ is the ratio of heat leaving the pipe by convection to the heat entering the pipe with the fluid flow. The factor $PL$ is the total external tube area $A$. With the boundary condition $\Theta = 1$ at $X = 0$, we have the solution.

$$\ln(\Theta) = -\beta X $$

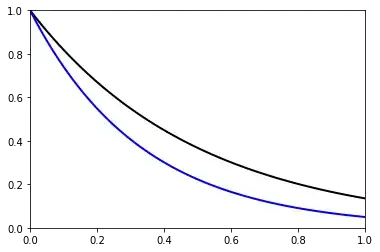
Here is a plot of $\Theta$ versus $X$ for $\beta = 2$ (black upper curve) and $\beta = 3$ (blue lower curve).

Typical Values

The pipe in your problem has a DIAMETER of 8 mm and a length of 4 m. This gives $A = (4)(2)\pi(0.004) = 0.1$ m$^2$.

Stagnate air outside the tube has a value $h_a \approx 5$ W/m$^2$ $^o$C [engineering toolbox]. Air has a specific heat of $\tilde{C}_p \approx 0.7$ J/g $^o$C [Ohio MAE Website].

Mass flow of air as an ideal gas is $\dot{m} = M(p\dot{V}/RT)$. At 25 $^o$C and 1 bar, this gives a relationship for mass flow (g/s) to volumetric flow (m$^3$/s) as below.

$$\dot{m} = 28(101325\dot{V})/((8.314)(298)) = 1150 \dot{V}$$

In the end, we have the relationship for $\beta$ to mass flow (g/s) or STP volumetric flow (m$^3$/s) as below.

$$ \beta = 0.71/\dot{m} = 6.2 \times 10^{-4}/ \dot{V} $$

Suppose we take a mass flow of 1 g/s of air through the tube. This gives $\beta \approx 0.7$.

$\Rightarrow$ To proceed further, we need the mass or volumetric flow through the tube.

Condensation of Water Vapor

Water vapor will condense when its partial pressure is equal to (or above) its vapor pressure. We can consider the Antoine equation to track the vapor pressure as a function of temperature.

$$ \log( p_{vap} ) = A - \frac{B}{C + T} $$

The first relationship we need to make is to translate the curve of $\Theta$ versus $X$ to a corresponding curve of $p_{vap}$ versus $X$. For ease in what follows, define that relationship as $AE \equiv 10^{\log (p_{vap})} = f(\Theta)$. We can then use the relative humidity of the incoming air to obtain the $p_{H_2O}$ in the incoming stream based on it $p_{vap}$.

$$ p_{H_2O}(X = 0) = RH_o\ p_{vap}(X = 0) = RH_o\ AE(\Theta(X = 0)) $$

The incoming stream has an initial value of $p_{H_2O}(X = 0)$. We have a plot of $p_{vap}(X)$ from $AE(\Theta(X))$. When $p_{vap}(X)$ falls below the value $p_{H_2O}(X = 0)$, water vapor will condense. The analysis needed to find the point $X$ when condensation starts is left as an exercise.

Starting at the point where water vapor condenses, the latent enthalpy of the exothermic condensation will act as an additional heat source in the energy balance. The temperature of the air will fall less rapidly. This analysis is also left as an exercise.