4

I have these 2 problems to solve (on the image).

I have 9 stores that want different quantities of a product. The first store asked for 62 units, the second one 10 units, etc etc.

The supplier sent a total of 138 units (case 1). I have to distribute those 138 units to all the stores in a fair way. Each box sent from the supplier has 2 units and it's better to use multiples of 2 units for each store, so that it's not necessary to dismantle the box. If it's not possible, we can dismantle the box but just in the last case.

In case 2, there are some stores who will get less than what they asked. That's ok. I just need to distribute them in a fair way so one store doesn't get everything and the others nothing.

I have a way to do this but it's really complex and full of errors so I'm trying to find an easier way like a formula or something.

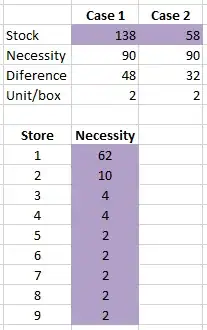
Table

What I'm doing is (I'm going to give an example for the first line and Case2):

  1. Giving a box to every store so there is no risk to have one store receiving nothing.
  2. Calculate: NecessityByPriority = Necessity-1box = 62-2 = 60
  3. Calculate: PriorityEachStore: 60/sum(NecessityByPriority) = 60/72 = 83,3333%
  4. Calculate: PriorityUnits = PriorityEachStore*(Stock-9box) = 83,3333%*(58-18) = 33,3333 [the 9box corresponde to the number of units given in the first step: 9stores*2units each]
  5. Calculate: NumberBoxes = round(PriorityUnits/(Unit/box)) = round(33,3333/2) = 17
  6. Calculate: NumberUnits = NumberBoxes*(Unit/box) = 17*2 = 34
  7. Calculate the final quantity: NumberUnits+1box[given in step 1] = 34+2 = 36

In the case given there is not a great error but I am going to show you one with error above in a simulator I have done in Excel:

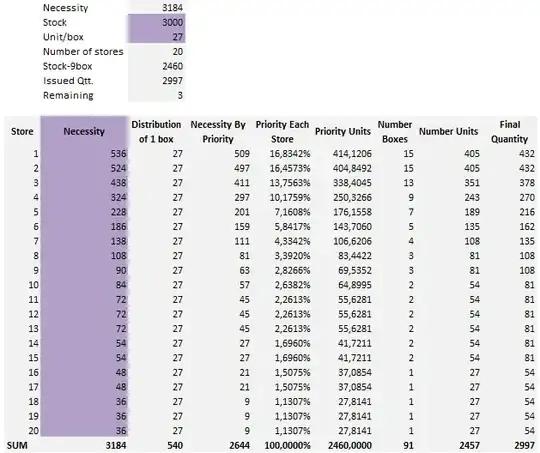
Table2

Here there were 3 units that remained. This is due to rounding. I can add a line to verify if there is something remaining and if so to redistribute. But I was looking for an easier way without all this formulas.

I have another process that calculates with the same formulas, everything for the first store. Then makes a 2nd iteration and recalculates everything except the first store. And on on until there is no more store. The problem is that here there is only 9 stores but sometimes there are hundreds.

hazzey
  • 10,682
  • 9
  • 42
  • 93
Pat
  • 57
  • 2
  • 2
    This smells like a combination of traveling salesman and knapsack (both NP complete) – ratchet freak Apr 24 '15 at 14:20
  • 1
    I'm voting to close this question as it does not deal with an engineering issue. It is a mathematics issue associated with distribution. It also looks like a homework problem. – Fred Apr 24 '15 at 14:45
  • 1
    Looks like an optimization problem: find the distribution that minimizes some penalty function (supply vs. demand + aversion to breaking up boxes). Can you try to quantify the relative 'cost' of under-supplying stores and relate that to the cost of splitting up boxes? – Dan Apr 24 '15 at 15:13
  • 3
    @Fred Optimization is a topic that happens to be incredibly useful across a broad range of modern engineering applications. So this question is a) useful to this audience and b) one that our users may be well qualified to answer. I'm referencing the reasons that a [conceptual question on the N.S. equations](http://meta.engineering.stackexchange.com/questions/266/is-this-question-on-the-navier-stokes-equations-on-topic) was deemed on-topic. – Dan Apr 24 '15 at 15:43
  • 1
    Without a definition of how you evaluate fairness, this is a non-question. With a proper definition it is merely a optimization problem with any number of common methods that can be applied to solve it. It's unclear which of these you are really asking about. – Olin Lathrop Apr 24 '15 at 20:30
  • This is a very good question. Manufacturing & Operations engineering handles similar type of scenarios all the time. These type of infomation are feed into design engineers when come to product design. A good answer from this question will benefit design for manufacture (DFM) frame work. Keep this question open – Mahendra Gunawardena Apr 25 '15 at 12:01
  • @OlinLathrop I answered that above – Pat Apr 27 '15 at 10:08
  • No, the point is you didn't. All you said was one store shouldn't get all. There are still many possible strategies. You first need to decide what metric you use to be "fair" so that you can put a numeric quality level on any particular distribution. – Olin Lathrop Apr 27 '15 at 12:21

4 Answers4

5

What is Fair?

Your definition of fairness is the quantity that you are really trying to optimize (maximize). There can be multiple methods to optimize for this, but first you have to define how this will be calculated.

I am going to describe some possible methods below.

Maximize Number of Full Orders

This method assumes that the happiness of each consumer is weighted the same. Because of this, you want to maximize the number of full orders.

Order the consumers from least requested to most requested and start filling orders from the top. This will give you the most completely filled orders.

Maximize the Biggest Orders

This methods assumes that the consumers that ordered the most are the most worthwhile consumers to keep supplied. You want these important consumers to be happy because you don't care about the smaller ones.

Order the consumers from most requested to least requested and start filling orders from the top. This will make the biggest consumers the happiest.

Fulfill the Same Percentage of All of the Orders

This looks to be the method that you tried to use. This one is more complicated, because you will end up with partial units.

Sum all of the orders and give a weight to each order based on the individual order divided by the sum of all orders. This is the percentage of the total available that each consumer will get.

This could be considered the most fair, but it isn't necessarily the best from a business standpoint.

Choose what to Optimize

You need to decide on what is to be optimized in order to be able to optimize the distribution. In this answer I have made some assumptions about the situation. I mostly came at the question from a business point of view, but the answer could be completely different if you were looking at supplying machines or if there were costs to not supplying some consumers. All of these issues will change the final solution.

hazzey
  • 10,682
  • 9
  • 42
  • 93
  • I think what adjusts more to my necessity is the third one. What I don't want is to give 1000 to the first store and the last one only receives what asked (in case where stock > necessity) or to give the first store 500 and the last one 0 (in case where stock < necessity). And in this case, those stores are all from the same company, just located in different places. And the store that is in first place this week can be last the next one. Each store asks for how much of an item needs for that week and that can change every week. – Pat Apr 27 '15 at 08:42
  • @Pat do you track the weekly demand for each store? If so can you post a few the weekly demand statistics for about 2-3 stores. I believe this is not very difficult problem to solve. – Mahendra Gunawardena Apr 27 '15 at 10:37
2

First, do away with "one for everyone" as the primary ones will be left with empty stock and the marginal ones with unsold ones.

Distribute according to your "Same Percentage of All of the Orders" method, rounding it down; assigning maybe 95% of the number you'd be able to assign.

Then dispatch the remaining units to stores that issue individual requests, per-request basis, first-come, first-served, depending on their individual demand - actual orders from the customers, not just "want to have it in stock".

The "necessity" distribution is subject to random fluctuations; you optimize basing on predicted demand that is subject to randomness when it comes to the actual sales. By delaying distribution from the "reserve cache" until there's a confirmed demand you fill these gaps in demand, making sure that all stores actually run out of stock at the same moment and in the final phase they all run on the reserve.

SF.
  • 6,153
  • 23
  • 43
0

Background

This question has been answered using lean manufacturing engineering concepts. I have used Toyota Manufacturing as basis for the solution. The idea can be applied to any other manufacturing engineering process such as pharmaceutical, consumer electronics, textile, or any other similar industry. Since this is an engineering forum, I have attempted to answer in an engineering frame work. The question could be answered in a pure business frame work too.

Response

Supplying raw material to manufacturing plant such Toyota Assembly plant has very similar correlation to supplying merchandise to a store. It is critical that all required parts be in stock in an assembly plant to a manufacture product, similar to having merchandise on shelf in a store to allow the consumer to make purchase. It is said that GM would lose over half millions US dollar if the Covert plant in Bowling Green Kentucky is not in operation for an hour.

enter image description here

A product/raw material required for the assembly of Toyota automobile is coolant temperature sensor. I have assumed that all the assembly plants listed below require a coolant temperature sensor. The fictitious volumes per month are also listed.

\begin{array}{| l | l | c |} \hline Toyota \ Manufacturing & Model & Average\ Sensors\\ & & required\ per\ week\\ \hline Mississippi & Corolla & 7500\\ Kentucky & Camry & 750 \\ Texas & Tacoma & 75 \\ Indiana & Sienna & 8 \\ \hline \end{array}

Using data engineering or information engineering statistical data tools and chart like individual moving range charts (I-MR)

enter image description here

Statistical tools such as the above will help determine the average pull rate (demand), standard deviations, and other information to determine minimum amount to product/raw material required to successfully operate the engineering manufacturing plant. Similar concept can be adopted to understand the demand in the stores.

From the supply side, demand averages, upper and lower control limit (LCL) is used to distribute the raw material to engineering manufacturing locations. The LCL will help determine with some level of confidence the minimum level of required raw material as well as strategy to distribute additional raw material.

Summary
If information such as standard deviation, UCL, LCL, median and range are added to the above Toyota Manufacturing Plant Temperature sensor weekly requirement table a great deal of insight to plant operation can be made available how best to distribute supplies. A combination of Data Engineering, Information Engineering, Process Engineering and statistics can greatly benefit toward optimization of the distribution process.

Mahendra Gunawardena
  • 7,153
  • 5
  • 25
  • 65
0

All the answers so far have taken the single-process deliberately planned approach. The way this problem is solved in many real life applications is to use distributed processes each attempting to locally optimize but competing with each other. As a result, the optimum distribution falls out almost as a bi-product.

Put another way, raise the price until demand is reduced to equal the supply. Even this system can be more distributed by using a method known as "auction".

Put yet another way, instead of the communist solution you seem to be asking about, you should also consider the capitalist solution.

Olin Lathrop
  • 11,351
  • 1
  • 20
  • 36