4

Assume I have a honecomb(sandwich) panel under distributed normal load. Each edge of this panel is simply supported(pinned) as on the picture below:

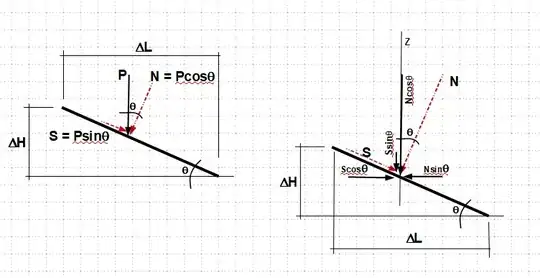
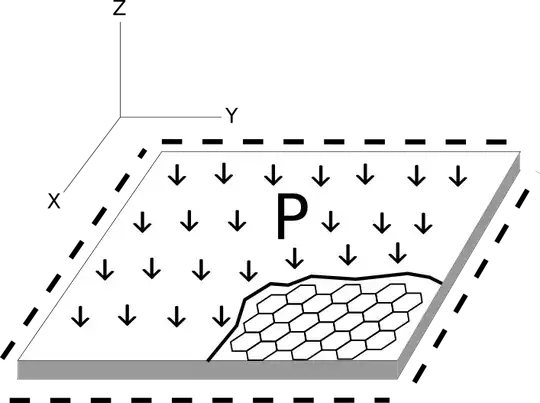
panel under normal load P

The problem is how to find the core stresses σ-z (not on sides of the panel) as on the picture below:

core stress σ-z

Also it will be very useful if you present some equations that describe σ-z in an ordinary (not honeycomb) panel. I'll be very pleased if you recommend some literature.

Eugene
  • 73
  • 2
  • Strength of Materials by Timoshenko. see http://www.engineering108.com/Data/Engineering/Mechanical/SM/Strength_Of_Materials_parts_IandII-Timoshenko.pdf – Solar Mike Apr 16 '19 at 08:56

2 Answers2

1

This is just "stress = force / area" where the area is the cross section area of the honeycomb walls.

The data sheet for the honeycomb will give the wall thickness. To understand the data sheet, you need to know how honeycomb is manufactured: flat strips of material are bonded together in the appropriate places, and the pack of strips is them pulled apart to create the hexagonal spaces.

So the wall thickness in one of the three directions along the sides of the cells is double that in the other two directions, because that is where the strips were bonded together.

If all the cell walls were thickness $t$, each individual cell would be surrounded by a wall of thickness $t/2$ (since each wall is the boundary of two cells), but in fact two parallel walls of each cell have thickness $2t$ not $t$ so the "average" wall thickness surrounding an individual cell is $2t/3$ not $t/2$.

alephzero
  • 12,587
  • 1
  • 12
  • 27
  • 1
    Panel is not lying on some surface. Only the edges of panel are pinned, but the whole area is free to move along z axis and it has some bending. In that terms i can't just compute stress = force / area. I shoud somehow connect the stresses with curvature. – Eugene Apr 16 '19 at 10:56
  • That curvature you are referring to sounds more like buckling of the individual panel faces. However, even if buckling is occuring still the macroscopic stress of the structure still remains force/area. Are you are more interested in localised stresses, in order to predict failure? – NMech Sep 07 '20 at 14:34
1

The illustration below is in response to your comment on alephzero's answer.

I think you are confused with the stress on an inclined plane, after ddelection/rotation, that will have the force components $N $&$ S$ as shown. Assume a finite strip with unit width,

in direction of $"Z", A_X = 1 * \Delta L = \Delta L$,

$\sum \delta_Z = N cos\theta/\Delta L + S sin\theta/\Delta L = Pcos^2\theta/\Delta L + Psin^2\theta/\Delta L = P/\Delta L$;

in direction of $"X", A_Y = 1 * \Delta H = \Delta H$,

$\sum \delta_X = N sin\theta/\Delta H - S cos\theta/\Delta H = Pcos\theta\sin\theta/\Delta H - Psin\theta\cos\theta/\Delta H = 0$

So the conclusion is that the compressive stress under the vertical force $P$ is uniform over a finite length of $\Delta L$ in each direction, or the stress is uniformly throughout the contact area if P is uniformly applied pressure.

enter image description here

r13
  • 7,917
  • 3
  • 8
  • 27