0

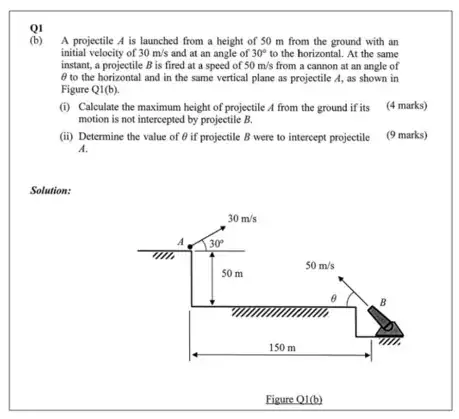
enter image description here

Hi everyone,

How do I approach questions like part (ii)?

From what I understand now, I believe the shortest method is that as long as the ANGLE of the relative velocity of B with respect to velocity of A is = Angle of thetha which in this case is arctan(50/150)?

Is this correct?

Another method I tried was to find the time taken for projectile and intercepter to reach the same x coordinate and use this to obtain the time in terms of thetha. Then I equated the y coordinate using this time in terms of thetha but I ended up being unable to solve them with 10sin - 10/3cos sin + cos = sqrt(3) + 3

What other ways are possible as well?

Thank you

Ong Chee Wei
  • 1
  • 2
  • The motion of such projectiles is never linear, but [parabolic](https://en.wikipedia.org/wiki/Projectile_motion) – Fred Apr 27 '19 at 09:35

2 Answers2

1

First, use consistent angles. Define $\theta^*$ to be the supplementary angle to the one illustrated.

For an intercept to occur, $x_A(t) = x_B(\theta^*,t)$ and $y_A(t) = y_B(\theta^*,t)$ for some $\theta^*$ and time $t$.

Taking $A$ as the origin -

$$x_A = 30 cos(30) t \qquad\qquad\ y_A=-1/2gt^2 +30sin(30)t\qquad$$ $$x_B = 50 cos(\theta^*) t + 150 \qquad y_B = -1/2gt^2 + 50sin(\theta^*)t - 50$$

Solve for the angle and time, and don't forget to change the angle back to it's supplement.

Phil Sweet
  • 4,130
  • 7
  • 15
  • isn't xB=150 - 50cos(θ∗)t ? and i think this is my 2nd method which resulted in 10sin - 10/3cos sin + cos = sqrt(3) + 3 – Ong Chee Wei Apr 29 '19 at 04:40
  • @OngCheeWei Thetastar is the supplementary angle to theta, so the cosine's sign changes. Yours is correct for the angle shown in the illustration. But often you have a lot of angles, and it is good to get into the habit of running all of them ccw from the x axis in the x - y plane. – Phil Sweet Apr 29 '19 at 10:14
0

You can write the parametric equation of trajectories:

$$y= -1/2gt^2+v_{y_{0}}t+y_0 \quad and\quad x= v{x_{0}}t+x_{0}$$

for the A it is,

$$y_A=-1/2gt^2+1/2*30*t+50 $$ And for B,we just use sin(theta)

$$ y_B=-1/2gt^2+50*sin(\theta)t+0 $$

We eliminate t and find the tetha.

Then we plug in the below equations to find t and x.

$$ x_B=150- 50 cos(\theta)t$$ And $$ x_A = 30 cos(30)t+0$$ $$150-20cos(\theta)t =0 \quad cos(\theta)t=7.5$$

kamran
  • 21,714
  • 2
  • 18
  • 38
  • Tetha aka theta? – Solar Mike Apr 27 '19 at 07:14
  • Thanks Solar Mike. I corrected the spelling. – kamran Apr 27 '19 at 07:20
  • no, kamran, this isn't sufficient. To effect an intercept, both the x and y components have to match at the same time. The variables available are theta and time. You can't eliminate time, you need it. The yb formula is missing a 2. Lastly, you need to make the trig consistent with the angles as drawn or redefine the angles to be consistent. – Phil Sweet Apr 27 '19 at 16:50
  • Phil Sweet, it is obvious that x, y, t should be the same. We have 3 unknowns and 3 equations. I will finish it if OP asked. – kamran Apr 27 '19 at 16:57
  • Three edits and it's still not right. You can't eliminate t and find theta. You have only one formula that looks like 50sin(theta)t = 15t+50. – Phil Sweet Apr 27 '19 at 17:42
  • I tried this method to check which resulted in 10sin - 10/3cos sin + cos = sqrt(3) + 3 but I dont know how to solve it – Ong Chee Wei Apr 29 '19 at 04:38