3

started by designing the gear meshing, and now I need to calculate some parameters to determinate if this meshing works for me.

The system considers an electric motor, which technical parameters are: - Power supply: 220V/50 Hz - Motor power: 180W

According to what I been studying, I start by calculating the T input (no-load) of the electric motor. For a 50 Hz three-phase supply and 2 poles: T = 50(Hz) * 60 (s/min) * 2 (Neg-Pos pulse) / n° poles = 3000 RPM Considering a slip speed of 6 - 7%, I end up with 2750 RPM (no-load)

Tinput = 0.241384 (lbf.ft/min) * 5252 / 2750 = 0.46 (ft.lbf) = 0.57 Nm

Now, my question is; Which is the relation between gear ratio and RPM to find the T output? What do I need to calculate the Torque output?

I know that when the gear ratio increase, usually the rpm decreases and the torque increase.

My goal is to move a gate of 600 Kg with a speed between 18 mts/min - 20 mts/min.Calc

Joaquin Osses
  • 185
  • 7

3 Answers3

2

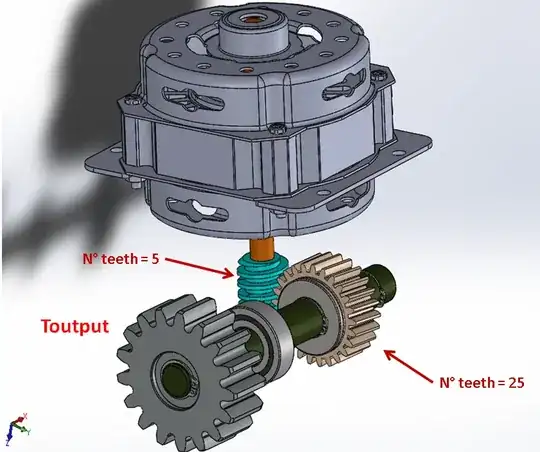
The transmission ratio is related to the number of teeth on the worm gear, and the number of starts on the worm.

In your case, $$i=\frac{z_{worm\ gear}}{z_{worm}}=\frac{25}{1}=25$$.

This means that you have a reduction of $25:1$, so, assuming $100\%$ efficiency, you would expect your output Torque to be 25 times higher than your input torque, and your output speed to be a twentyfifth of your input speed. $$T_{output}=25T_{input}\ ,\ \omega_{output}=\frac{\omega_{input}}{25}$$

This relationship will hold pretty much true for the speed ratio, although you will find that resistance from the gears and the load will reduce your input speed to be lower than you have calculated above. You can get an estimate for the expected motor speed by looking at its datasheet.

For torque, however, you need to account for lost power to e.g. friction.

According to: https://www.machinedesign.com/mechanical-drives/gear-efficiency-key-lower-drive-cost

Efficiency of a worm-gear speed reducer depends (in part) on its speed-reduction ratio. High-ratio units have a smaller gear-tooth lead (helix) angle, which causes more surface contact between them. This higher contact causes higher friction and lower efficiency. Typical worm-gear efficiencies range from 49% for a 300:1, double-reduction ratio, up to 90% for a 5:1, single-reduction ratio.

So, with your ratio of 25:1, it seems safe to guess at an efficiency around 80% as a starting point.

Looking at conservation of Power, including Losses,$$P_{in}=T_{in}\omega_{in}=T_{out}\omega_{out}+\left(0.2*P_{in}\right)$$ Therefore $$T_{out}=\frac{0.8*P_{in}}{\omega_{out}}=\frac{25\left(0.8*P_{in}\right)}{\omega_{in}}=\frac{20*P_{in}}{\omega_{in}}$$

Re: your goal of moving a 600kg gate - you need to consider acceleration as well as just 'cruising speed' when doing your power calculations.

Jonathan R Swift
  • 7,727
  • 1
  • 14
  • 27
  • In my experience worm gear efficiencies are much lower than that unless you're using exotic lubricants. As a quick check, if the driving efficiency is less than 50%, then you can't back-drive the gear -- and that's pretty common. – TimWescott Jul 25 '19 at 18:58
  • Ok, according to you solution for the output; Tout = 20*180 (kg x m x rpm)/2750 rpm = 1.3 Kg*m...How do I use this value to know if I can move the 600 kg at 0.3 m/sec? Regarding acceleration; if I use kinematics I know that w^2= w_o^2+2∝θ, can I use this equation to calculate the acceleration, knowing that w_o^2 = 2750 rpm and w^2 = output rpm? – Joaquin Osses Jul 25 '19 at 19:27
  • Not quite - I've defined $P_{in}=T_{in}\omega_{in}$, but you've used 180W, which is the electrical power in - the motor is not 100% efficient. – Jonathan R Swift Jul 26 '19 at 07:30
1

The gear ratio is the slope of worm gear per teeth of the round gear, so if one rotation of the worm gear turns two gears down on the round gear you have a ratio of

$\frac{1}{(25/2)}= \frac{1}{12.5}.$

So you have to set this ratio according to the torque you need, same worm gear engaged to a round gear with more teeth is more torque, less speed.

You then multiply this by the efficiency of your gear system, which has to do with the quality and finish of the gears, lubrication, and the friction in bearings and housing.

as for the ratio of the torque,

Let's assume the gate takes 3 seconds to reach the speed of20meters/mins =1/3m/s so your acceleration is (1/3) /3=1/9ms.

$$F=m* \alpha = 600*(1/9)= 66kgm= 645N force.$$

You have to figure out what mechanism you want to use to impart this force by using the torque of your electrical motor. Are you going to use a chain drive or crank arm. then you calculate the mechanical advantage of those.

kamran
  • 21,714
  • 2
  • 18
  • 38
  • By "set this ratio according to the torque you need" you mean; Tout = (1/12.5)Tin ? – Joaquin Osses Jul 25 '19 at 20:13
  • No. I just gave the ratio as an example. You set the ratio by choosing the gears. – kamran Jul 25 '19 at 20:15
  • Ok, understand. In the final equation by assuming a 3 sec for the gate to reach a peak of 0.3 m/sec. The F needed to move the 600 Kg gate must be; 600 kg x (0.3 m/s / 3 sec) = 66 N. If the distance between the gear mesh and the spur is around 15 cm, the Tout must be; T = 66 N * 0.15 m = 9.9 N.m. So I need to find a gear ratio which satisfies this Tout – Joaquin Osses Jul 25 '19 at 21:44
  • I think you got it. My apologies i am in a meeting. Just remember your system has a few levers and gears. The final torque is the sum of all those and each components frictiion. – kamran Jul 25 '19 at 22:13
1

You got good answers here, however, I think another little push is still needed.

I suggest to examine the whole mechanism, end to end. Do you intend to drive the gate by a rack and pinion mechanism?

rack and pinion illustration from wikipedia

First we need to estimate the force, speed and power needed to drive the gate. Let us conservatively assume a 0.1 friction coefficient between the gate and the ground (I guess the gate supported on wheels so practically the coefficient is much smaller) - that brings us to about 600 [N] needed for pushing it (600 [kg] times 9.8 [m/sec^2] times 0.1). You also mentioned that the required linear velocity of gate is 0.33 [m/sec]. Putting it all together, the needed power for driving your gate is P = f*v = 600 [N] times 0.33 [m/sec] = ~200 [W]. We still have not taken into consideration power losses along our system, so you should re-thinking about the choice of your motor. However, let's continue with the system analysis.

Do you know the size of your pinion or you have to adjust it yourself? The rack and pinion interface convert the linear motion to a rotational motion. Thus, if the pinion radius is 24 [mm] (I purposely chose it to adjust the numbers) and the linear velocity is 0.33 [m/s] - the desired angular velocity of the pinion is 0.33 [rad/sec]/0.024 [m] = 13.75 [rad/sec] or 131 [RPM]. Similarly, the Torque the pinion has to deliver for the rack to apply 600 [N] is 600 [N] * 0.024 [m] = 14.4 [Nm].

As @Jonathan R Swift explained, the worm gear ratio in your case is 1:25 so ideally the motor should deliver 0.576 [Nm] at 3275 [RPM].

Next, we have to estimate the efficiency of both gear system. Efficiency of 0.95 is quite reasonable for spur gears while 0.5 efficiency would be a good guess for the worm (sometimes worm gears have even lower efficiencies). Furthermore, while the speed is not effected by the gear efficiencies, the motor shall supply higher torque in order to meet your requirement. Therefor, The needed motor torque is 0.575 [Nm] / (0.95*0.5) = 1.21 [Nm].

This calculation has to be repeated for the gate acceleration, as already discussed here by @kamran

Yaniv Ben David
  • 448
  • 4
  • 13
  • Your suggestion is correct. The whole mechanism considers a Rack and a pinion to move the 600 kg gate. I have a few questions, though. Why do you find gears efficiency separately; 0.95 for spur and 0.5 for a worm? Second, I forgot to mention that I have the flexibility to change components. I mean if it's better to change the motor, or the reduction gears to achieve the goal which is to move the gate at 0.33 m/sec. Could you help me to understand the gate acceleration calculation, as @kamran proposed? – Joaquin Osses Jul 26 '19 at 13:51
  • Different gears have different efficiencies - The shape and implementation of a worm gear is quite different than a spur gear. You can find here a nice comparison: https://www.meadinfo.org/2008/11/gear-efficiency-spur-helical-bevel-worm.html Regarding the components - first you have to verify that your motor has enough power to drive the system. If its power capability is high enough, you can adjust the torque and speed to meet your wishes. Regarding the acceleration: again, you have to start your calculation by finding the speed and force. F=m*a will do that, when a is the desired acc... – Yaniv Ben David Jul 26 '19 at 14:16
  • As you well explained, the motor that I have not to supply the power enough to move the 600 kg at 0.3 m/sec (194 W). You assumed a 0.1 friction factor but supposed that's ok (I didn't find a table for friction factors). But what if, I want to keep the motor and change the gear parameters (n tooth, lead angle, etc.). How do I know which gear ratio I need to accomplish my goal? Is it's that possible? – Joaquin Osses Jul 26 '19 at 14:44
  • I intentionally kept the efficiency calculation to the end of my explanation. You can deduce that the motor doesn't have enough power - this holds forever, no matter what kind of gears you choose. After you come up with a motor that can supply enough torque, we can go on. O.K? – Yaniv Ben David Jul 26 '19 at 15:00