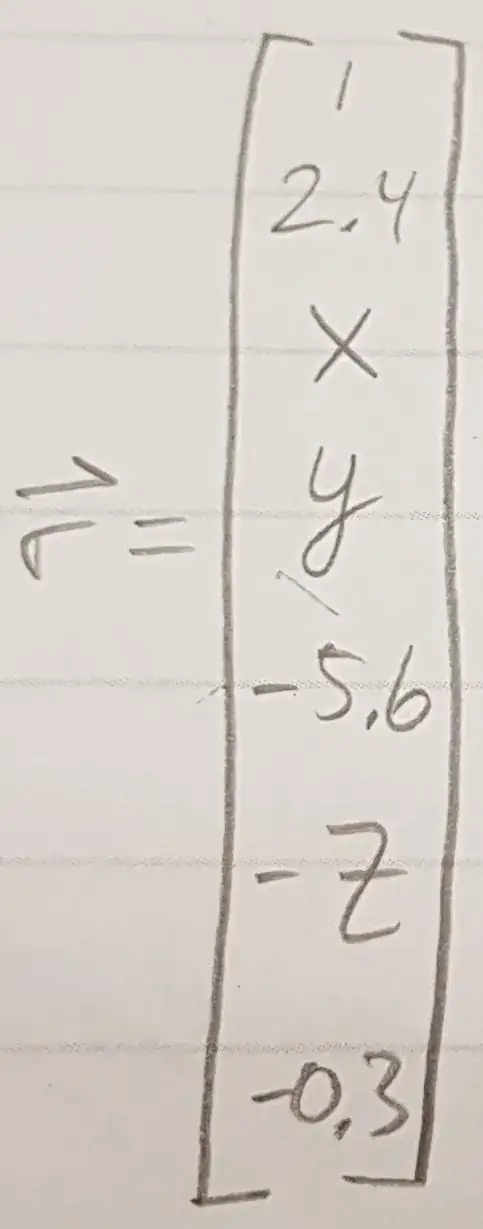You don't need a computer program to solve this. You can almost do it in your head.
The last equation is satisfied by any values of $x, y, z$ so you can forget about it.
If you multiply out the first row of the matrix product, you get $$1 + 2.4 + x + 0 -5.6 + 0 + 0 = 0$$
which is pretty easy to solve for $x$.
The second row is just as easy to solve for $y$, and the third row gives you the value of $z$.
If you have several sets of equations like this to solve with different coefficients in the $E$ matrix, you can rearrange the equations in the form $$\begin{bmatrix} a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}
\end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} =
\begin{bmatrix} c_{11} & c_{12} & c_{13} & c_{14} \\
c_{21} & c_{22} & c_{23} & c_{24} \\ c_{31} & c_{32} & c_{33} & c_{34}
\end{bmatrix} \begin{bmatrix}d_1\\d_2\\d_3\\d_4\end{bmatrix}$$
and you should then be able to find some routines to multiply the $C$ and $D$ matrices and then solve the equations.
A different way to solve this by computer is to consider all 7 elements of the vector as variables, and then add more equations which give them their known values. That would give a set of 7 equations like $$\begin{bmatrix}
1 & 1 & 1 & 0 & 1 & 0 & 0 \\
2.3 & 3 & 0 & 1 & 2 & 0 & 3 \\
0.8 & 0.5 & 2 & 1 & 1 & 2 & 0 \\
0.3 & 0 & 0 & 0 & 0 & 0 & 1 \\
1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 \end{bmatrix}
\begin{bmatrix} a \\ b \\ x \\ y \\ c \\ -z \\ d\end{bmatrix} =
\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 2.4 \\ -5.6 \end{bmatrix}$$
where the three additional equations fix the valued of $a, b, c$ (and the fourth equation, which was irrelevant for finding $x, y, z$, will give the value of $d$).