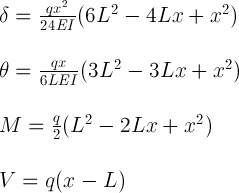Hey, I make a project in which I use a cantilever beam with distributed equal load across the whole beam and I'm using the formulas above to calculate the displacement, moment...
My specifications for the beam are: 4.5m long aluminum 2024 beam, 4x3 cm walls (the force is applied on the 4cm side), 2mm thickness. and a young's modulus of 70 GPa. a force of 40 N/m is applied
from my calculations the moment of inertia is 37 mm^4, meaning the maximum displacement should be 0.6m at X=4.5 and the maximum moment is 400 N-m at X=0.
When I put the results in the formula for bending stress, the maximum bending stress is 162 MPa, while the yield stress for this type of aluminum is around 300 MPa.

something here doesn't seems right for me. the beam is bent 0.6m but does not exceed the yield point, maybe I did a mistake somewhere?