1

Hello everyone :) This is my first post here so please excuse any of my mistakes.

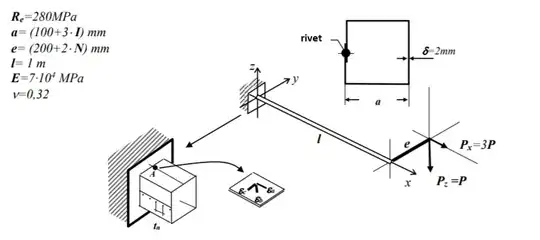
I’m having some difficulty with solving the following problem. Let us have a thin-walled square pipe exposed to bending, torsion and stretching (picture below). On the left side of the pipe, where sits the rivet, we will have shearing stress due to the twisting moment and the shearing force coming from the bending moment. At the exact same point we will also have normal stress coming from the streching and bending moment.

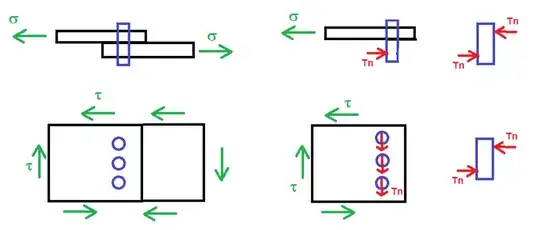
While calculating the force in each rivet, why do we only consider shearing stress without the normal one? I tried asking my professor. He replied with the second attached picture, which I don’t seem to understand. Any help is appreciated :)

enter image description here

His response

EngineerInProgress
  • 143
  • 6
  • 1
    Rivets are joining devices for devices that act as plates, sheets or thin walled tubes. Any lateral stresses in the plates/sheets or thin walled tubes is experienced as a sheer stress by the rivets. The only way to get a normal stress on a rivet is to apply an external stress directly to the head or bottom of the rivet, longitudinally to the rivet such as hitting the rivet with a hammer. – Fred May 30 '20 at 00:27
  • @Fred thank you for your answer! I'm still not sure about one thing though. Would you be so kind as to explain why the sigma's (representing normal stress) on my professor's drawing are suddenly changed to Tn's (shear force)? Do you know what he could have meant? :) – EngineerInProgress May 30 '20 at 06:42
  • 1
    The sigmas for the plates represent stresses in the plates, they could have easily been represented as forces. When those stresses are transferred to the rivet the effect is the top plate is trying to pull the rivet to the left, while the bottom plate is trying to pull the rivet to the right. The effect of this is a cutting or sheering action against the rivet. The stresses on the rivet are acting against the cross section of the rivet. – Fred May 30 '20 at 11:15
  • @Fred Thank you for taking your time to reply :) I think I'm missing some IQ point for im still not sure of one thing. If our thin walled tubed was only streched we would still get sigmas (just like on the second picture), but no shear force. In other words I just find it non-intuitive that sigmas from the second pic give us shear force... I thought that shear stress (denoted by tau) is the one responsible for giving us shear forces, not sigmas. Sorry to be a bother. Thanks again :) – EngineerInProgress May 30 '20 at 15:23
  • 1
    The sigmas are acting longitudinally within the plates. Where the sigmas in the plates contact the rivet they act across the cross section of the rivet, not the longitudinal direction of the rivet. Because the rivet "contact stresses" act across the cross section & from **both sides of the rivet from opposite directions** the stresses are effectively trying to force top part of the rivet to slide away from the bottom part. This is a shearing (or cutting) action & thus the resultant stresses acting on the rivet are shear stresses, even though they may have been tensile stresses in the plates. – Fred May 30 '20 at 19:01

0 Answers0