A clarifying question on Lasalle invariance principle

Question

Given a nonlinear system \begin{equation} \dot{x}=f(x),~x(0)=x_0 \tag{1} \end{equation} where $f\in{\mathcal{C}^{1}}:D\to\mathbb{R}^{n}$. The Lasalle invariance theorem statement goes as follows:

Let $\Omega\subset{D}$ be a compact set that is positively invariant with respect to (1). Let $V:D\to{\mathbb{R}}$ be a continuously differentiable function such that $\dot{V}(x)\leq{0}$ in $\Omega$. Let $E$ be the set of all points in $\Omega$ where $\dot{V}(x)=0$. Let $M$ be the largest invariant set in $E$. Then every solution starting in $\Omega$ approaches $M$ as $t\to\infty$.

Here $M$ is the largest invariant limit set (every invariant set is a subset of M) where $x(t)$ converges to at infinite time. My question is how is $M$ and $E$ different. Since $\dot{V}$ is zero at whole of $E$, then isn't $E$ itself the largest invariant set?

Answer 1

A set is invariant with respect to its dynamics if $x(t_0)\in M \implies x(t)\in M$, this is not the case for the set $E$. The set $E = \left\lbrace x\in \Omega \mid \dot{V}(x) = 0 \right\rbrace$ does not need to be an invariant set, since it does not consider the solution of $x(t)$.

I'll show this statement using the well known pendulum example. The dynamics of a pendulum with friction are given by $$ m\ell^2 \ddot{\theta} +d\dot{\theta} + mg\ell \sin(\theta) = 0, $$ and in state space form by $$\dot{x} = f(x) = \begin{bmatrix} x_2\\ -\frac{g}{\ell} \sin(x_1) - \frac{d}{m\ell^2} x_2\end{bmatrix},$$ where $x_1 = \theta$, $x_2 = \dot{\theta}$. The equilibria are $\bar{x}_1 = k\pi$, $k\in\mathbb{Z}=\left\lbrace\ldots,-1,0,1,2,\ldots\right\rbrace$ and $\bar{x}_2 = 0$.

Now, take the energy as the Lyapunov function candidate $$V(x) =mg\ell\big(1-\cos(x_1)\big) + \frac{1}{2}m\ell^2 (x_2)^2$$ with its derivative $$\dot{V}(x) = \frac{\partial V}{\partial x}f(x) = -d(x_2)^2 \leq 0.$$

The sets in LaSalle's invariance principle are $$\begin{align} \Omega &= \Omega_c := \left\lbrace x\in \mathbb{R}^2 \mid V(x) < c\right\rbrace\\ E &= \left\lbrace x\in \Omega \mid \dot{V}(x) = 0 \right\rbrace = \left\lbrace x \in \Omega \mid x_2 = 0\right\rbrace\\ M &= \left\lbrace 0 \right\rbrace, \end{align} $$ where $M$ is the largest invariant set in $E$.

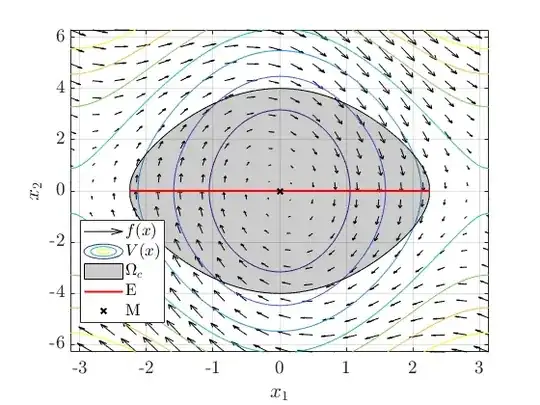
Now, consider the point $x = [1, 0]^\top \in E$, i.e. $\theta = 1$, $\dot{\theta} = 0$. This point is in the set $E$, however it will not stay in $E$ because the gravity will cause the pendulum to move, i.e. $x_2 \neq 0$ leaving $E$. Hence, for a point in the set $E$ it does not imply that $x(t_0) \in E \implies x(t)\in E$. This is visualized in the figure below by the vector field (black arrows) and the different sets. The vector field in $E$ is pointing away from $E$.

The vector field and sets below are drawn for $m = 1$, $\ell = 1$, $g = 9.81$, $d = 1$ and $c = 8$.

Answer 2

The sets $M$ and $E$ can be different. The set $E$ only considers $\dot{V}=0$ while $M$ also considers $f(x)$. Namely, invariant set means that for all $x(0) \in M$ the solution $x(t)\in M$ for all $t>0$, which can also be written as $x(0)+\delta\,f(x(0)) \in M$ for infinitesimally small $\delta$.

For example consider the system

\begin{align} \dot{x}_1 &= x_2 \\ \dot{x}_2 &= g(x_1,x_2), \end{align}

and there exists a $V(x_1,x_2)$ such that $\dot{V}=-x_1^2$. From this it would follow that $E$ only requires $x_1=0$ and $x_2$ can be anything. However, when considering the dynamics in order to keep $x_1=0$ it is also required that $x_2=0$, thus $M$ only consists of the point $x_1=0$ and $x_2=0$.