4

Is there a calculation / rule of thumb that can determine a containers rough maximum negative pressure (vacuum) from it's rated internal pressure (assuming a single layer construction so there is no additional bracing preventing expansion).

As an example for a 50 litre stainless steel keg (cylindrical with convex end caps) with an integral 580 +/- 140 psi bursting disc.

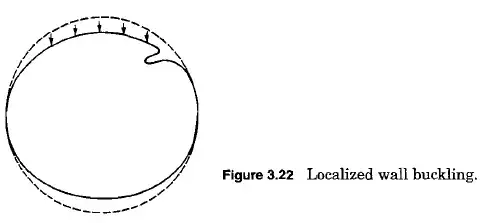
Would it be valid to assume that the weakest point (excluding the bursting disc) is calculated to withstand 400 psi of internal pressure (minus approx 14 psi from external atmosphere), directed outward so placing the material under tension. By reversing pressure differential (My logic says the weakest point still remains the same) the weak spot would come under a compressive force and the maximum pressure under vacuum would be a function of the ratio of that particular stainless steal grades tensile:compressive strength.

EDIT I just realized the bursting disc pressure is not relevant since that only indicates when a rupture would occur. In the reverse situation deformation into a flat can would occur well before then. However if instead of the bursting pressure you were to apply the 'Maximum working pressure' of 43.5 psi which presumably implies no deformation does the above apply?

grfrazee
  • 3,587
  • 1
  • 16
  • 33
norlesh
  • 285
  • 2
  • 10
  • @grfrazee's answer still applies after your edit. The maximum working pressure is usually obtained by the rupture internal pressure divided by some safety factor. In order to calculate the maximum allowable vacuum pressure, you'd need to calculate the rupture vacuum pressure and then divide that by the same safety factor. It might be (or just as easily not) that the rupture vacuum pressure is above the working internal pressure, which means it probably wouldn't implode, but you would not be "safe" according to the engineering definition of the term. – Wasabi Jul 23 '15 at 19:52
  • There is no certain internal to external pressure withstand ratio for an arbitrary vessel shape. This may exist for a very well defined profle. Consider a 1.5l PET softdrink bottle. They will tolerate 100 psi indefinitely, 150 psi often 200 psi seldom. But will buckle ("implode") under a few psi of suction.[Try pourng very hot water in a thin stream via funnel into bottle rapidly. Shake heavily once then seal. Observe as it cools]. – Russell McMahon Jul 24 '15 at 06:57

4 Answers4

5

Vacuum pressure on a vessel is quite different than positive pressure.

Under positive pressure, the shell of the vessel is essentially under a uniform membrane tension due to the shell wanting to expand outward from the pressure.

Under vacuum (negative) pressure, the opposite is true, where the shell is in compression. While a cylinder is stronger in this type of compression than, say, a flat plate, one cannot directly correlate the vacuum pressure capacity with the positive pressure capacity. This is due to the buckling failure mode of the thin shell under compression.

See this recent relevant SE Question.

Edit: As an additional illustration for the buckling failure mode, I present the following image from Buried Pipe Design, 3rd Ed., by Moser & Folkman. The design equations presented in that text for piping are not strictly applicable to your case, but the theory is similar.

enter image description here

grfrazee
  • 3,587
  • 1
  • 16
  • 33
1
Is there a calculation / rule of thumb that can determine a containers rough maximum negative pressure (vacuum) from it's rated internal pressure (assuming a single layer construction so there is no additional bracing preventing expansion).

Clearly not, as consideration of a few different cases makes obvious.

Consider a mylar balloon. It can handle some positive internal pressure, but it's ability to withstand negative pressure without collapsing is essentially 0.

On the other hand, consider a spherical steel tank. It can certainly take some negative pressure.

Clearly the relationship between maximum positive and negative pressure in these two cases is quite different, making the answer to your question "No".

Olin Lathrop
  • 11,351
  • 1
  • 20
  • 36
0

Failure of cylindrical shells under external pressure depends on length in addition to all the factors for internal pressure. If you can get your hands on a copy of the ASME boiler and pressure vessel code Section VIII division 1, and section II part D, you can calculate it yourself using the formulae in UG-28. Alternatively, there are a few pressure vessel software suites that offer free trials.

user2785724
  • 105
  • 3
0

I ran through once for atmospheric fiberglass tanks designed to hold specific gravity 1.2 (which corresponds to Hydrochloric acids, but can hold a wide variety of things). These tanks were sized for New York City Seismic Loading:

A 4' diameter x 4' tall atmospheric tank can withstand 27" w.c. of vacuum,

An 8' diameter x 8' atmospheric tank can withstand 4" w.c. of vacuum.

A 12' diameter x 12' atmospheric tank can withstand 2" w.c. of vacuum.

A 4' diameter x 8' tall atmospheric tank can withstand 14" w.c. of vacuum,

An 8' diameter x 16' atmospheric tank can withstand 2.4" w.c. of vacuum.

A 12' diameter x 24' atmospheric tank can withstand 1" w.c. of vacuum.

Bottom Line: While materials, thickness, etc. make the relationship between internal pressure design and external pressure design a blur, once you know what one vessel of a particular design and style can hold for both, it's pretty easy to scale both internal/external design parameters (and even Height-to-Diameter Ratio!) and find out what another similar tank will do.

Community
  • 1
Mark
  • 5,333
  • 13
  • 47