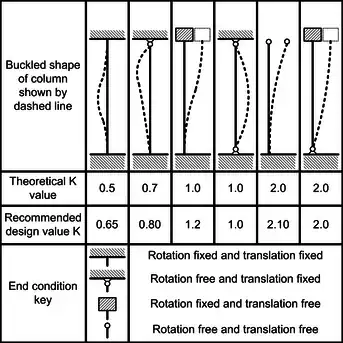
how can I calculate how many newtons a 600[mm] long rod with a known yield strength (300 [MPa]), young modulus (190 [GPa]) and hollow (outer diameter = 16[mm], inner diameter = 10[mm]) will carry without buckling?
Thanks.
Edit: My main question is "How do I use the yield strength in the Euler buckling formula? What does it do and how do I determine "Factor Counting for End Conditions" for suspension pushrods?