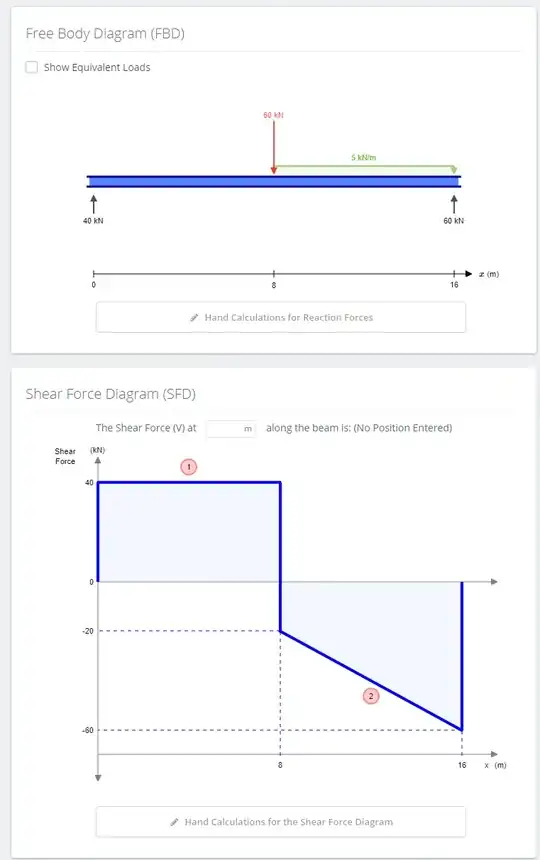
So here I have a cantilever beam and I have the shear force diagram. When we are talking about the maximum shear force diagram. Should I take 40kN? Or I need to absolute the value and take 60kN. I am new to mechanical engineering and I am so confuse on these kind of problem.
Get the absolute value, so the maximum is 60.
What defines whether a shear force is positive or negative? Is it something intrinsic to the force or the applied loading? Well, no. If it were, then indeed, the maximum force would be +40. But that'd mean that pushing down on a symmetric beam would break it at a different force than if you pushed up. But if that were the case, wouldn't that also mean that flipping a symmetric beam over would lead to a different maximum load than in its original position? But if that's the case, what would happen if I gave you a square beam? How would you define its upside up and upside down directions?
This starts getting silly, so we can basically discard that option. So if it isn't intrinsic to the loading, what is it?
The answer? It's entirely arbitrary. One direction of shear force is positive and the other is negative because we say it is. That's what we call a sign convention. Indeed, the complete standard sign convention for positive internal forces is the following:
But the convention could just as easily be inverted, since nature doesn't care about our stupid conventions.
So, if the convention is arbitrary, then the signs are arbitrary. And if the signs are arbitrary, they don't matter. If the signs don't matter, then -60 is greater than +40.
TL;DR: If your goal is to find likely points of failure, take the absolute value
It may seem I'm repeating what other have said. I'm merely trying to expand and I'll be trying to give another angle on this. Hopefully, some might find it helpful.
How we perceive Shear forces is different than tensile/compressive forces.
Tensile and compressive forces produce a visible and tangible result on the length (most of the times). Since length is one of the primary dimensions of a member, it is easy to associate elongation with the tensile, and length reduction with compression. Reversing the direction of the external load which causes elongation/reduction results in the opposite effect (i.e. reduction/elongation)
However, shear doesn't appear work this way. If I apply a load which causes shear, then if I reverse the direction of the load, the beam will just obtain the same shape, in the opposite direction (there is no visible/measurable change in any of the two deformed states). That is why, as Wasabi already explained, the sign shear forces is only a matter of agreement (a convention).
When you are trying to get the maximum shear in a member you are doing it (most likely) to find locations of possible failure. However, if you apply the loads in the opposite direction and you would still get exactly the same values, just with the opposite sign (if you followed the same convention. Therefore, if your goal is to find locations with high likelihood of failure, then just take the absolute value.
The section "feels" the maximum shear of -60kN at X=16m regardless of the sign of the shear. The three notable points along the beam's shear diagram are X=0 and X=8 and X=16 with corresponding shear values of +40kN at X0, +40 -20 at the left and right of X8, and -60kN at X16.
For the molecules of the beam direction of the shear is meaningless.
The section near X=16 must be strong enough to resist the 60kN shear trying to push the beam down.
