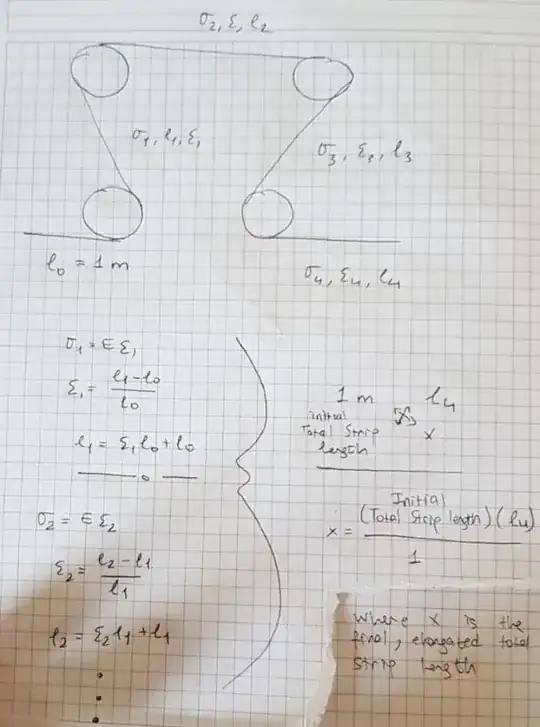
You have to remember that you can control independently (or with a fixed gear ratio), the rotational velocity for each roll.
So, in order to decrease the tension, what you do is you decrease the rolling speed progressively in the output zone.
A very similar concept which is under the same restrictions, is the belt pulley system. Below it shows the tension at each different section of the belt., assuming the small gear on the right is applying the input torque.
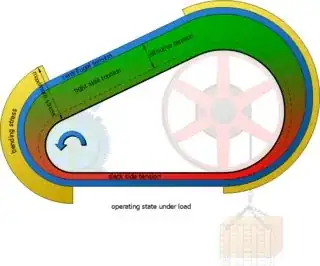
You see that the top side is under tension, while the bottom side is more (or can be almost ) relaxed. That tension results into deformation, and that deformation creates a different speed on the top and on the bottom side.
UPDATE: to address comments
The capstan equation is (as you rightly note in the comments) :
 $$T_{out} = T_{in}* e^{\mu* \phi} $$
where:
$$T_{out} = T_{in}* e^{\mu* \phi} $$
where:
- $\mu$ is the coeffiecient of friction,
- $\phi$ is the wrap angle in radians,
- e is the Euler constant
However, you did not mention, the other two important factors, namely:
- $T_{in}$ or $T_{Hold}$ : this is the force applied to one end
- $T_{out}$ or $T_{Load}$ : this is the force applied to the other end.
You need to note, that what the pulley does is that it magnifies the force opposite to the rotation by the factor $e^{\mu* \phi}$. However, if $T_{in}$ is zero then that means that $T_{out}$ will also be zero. So what really controls the $T_{out}$ force is the $T_{in}$.
However, $T_{in}$ can be controlled at a previous stage by adjusting how much feed, there is. So lets, say for simplicity sake that all rolls are 1[m] radius. And lets assume that Roll 1 (R1 for short) is rotating with $n_1=1$ [rpm], and Roll 2 with $n_2 = 1.001[rpm]$, and that the distance between them is exit of roll 1 and roll 2 is 1[m].
That means that between the exit of 1, and entering 2 the tape feed needs to grow by $\Delta L = (\frac{2\pi n_2}{60} R_2 - \frac{2\pi n_1}{60} R) \Delta t$ (where $\Delta t$ is a small timestep). That can be further simplified (to make the point more easily evident) because $R_1 = R_2 $ to:
$$\Delta L = \frac{2\pi R}{60} (n_2 - n_1) \Delta t$$
Therefore, (bypassing strain $\epsilon= \frac{\Delta L}{L}$, stress $\sigma = \epsilon E$, and $\sigma = \frac{F}{A}$ and going directly to ) Hooke's Law:
$$F= K \Delta L $$
where:
- $K = \frac{EA}{L}$: is the equivalent spring constant for the tape.
So you can see, by controlling the speed of the material on one stage you can create a tension. That tension is further increased/decreased at later stages, again depending of the feed rate (rotation of rolls).
Different type
if you are using the following type,
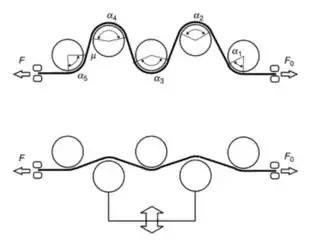
Then again, the initial tension is dominated by the speed difference in feed in and out. However you can increase the tension, by increasing the angle.