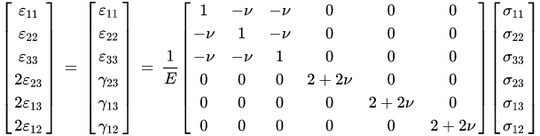What exactly is Hooke's law defined for?

Question

I used to think that Hooke's law was a relationship between how much a bar under uniaxial loading deformed and the internal force (per unit area) that developed within that bar. But this clearly isn't the case as I have recently seen that Hooke's law is used in analyzing the stress in pure bending of beams. So it seems that Hooke's law is a lot more general than I had thought.

If Hooke's law isn't specifically defined for a bar under uniaxial loading, what physical object is it exactly defined for? What system/object is Hooke's law trying to describe?

My guess is that Hooke's law is defined for an infinitesimal cubic element which feels a normal stress on its sides from neighboring elements (picture below). That is, Hooke's law relates the normal stress and normal strain on an infinitesimal cubic element. This might make Hooke's law general enough so that it could be applied to many loading situations since we can think of any object as being made of many of these infinitesimal elements and the total strain of the object is the sum of the strains of all of the elements. Is this correct? I'd appreciate it if someone could clear this up for me.

Answer 1

TL;DR: Hooke's Law refers to structures in general.

Hooke's law generally refers to following equation

$$F = - k x$$

In this (original) form there was no reference to stresses. Later, I suspect in order to honor Hooke's contribution you might see formulations such as the following.

In order to make things more clear a bit of history might be in order. Hooke was a very intelligent person, that was more inclined to solve practical problems (in many respects he was the archetype of an engineer).

---

(sidenote: That practicality -amongst other things (see dispute on contribution)- put him at odds with his contemporary Sir Isaac Newton. Newton, -as I understand it- had the view of a scientist. That things needed to be understood, and not explained. Also, according to some scholars Hooke and Isaac Newton disputed over credit for certain breakthroughs in physical science, including gravitation, astronomy, and optics. After Hooke's death, Newton questioned his legacy. And as the Royal Society's president, Newton allegedly destroyed or failed to preserve the only known portrait of Hooke. In the 20th century, researchers Robert Gunther and Margaret 'Espinasse revived Hooke's legacy, establishing Hooke among the most influential scientists of his time. see wikipedia on Robert Hooke).

---

Hookes experiment involved experimenting of combinations of different weights on a structure (he used different materials and shapes). What he discovered was that there was (most of the time) a linear relationship between Force and displacement of the structure. If I am not mistaken his experiments at the time were driven by his work to create a spring loaded lamp that was used in London up to almost 1900's (for almost 200 years). Hooke didn't bother to investigate further (Galileo also did similar work and failed to investigate deeper). In was approximately 100 years later that Augustin-Louis Cauchy first talked about what we know and understand today of stress, thus giving a way of decoupling geometry (A,L,I) and material properties (E,v,G).

So, bottomline, the idea behind Hooke's Law is very generic. It can be applied to most structures.

Answer 2

Hookie's Law defines the linear elastic relationship of material within the elastic range in the stress-strain curve.

$F = kx$

$k = EA/L$, so

$F = EA(x/L) = EA\epsilon$, and $F/A = \delta$, so

$\delta = E\epsilon$

Now we can generalize the "Hooke's Law" to cover the stress ($\pm\delta$), on an element of "homogeneous isotropic" material, resulting from any types of loading that produces a strain ($\epsilon$) in direct proportion to the intensity of the stress (linear), and the strain is recoverable upon unloading (elastic behavior) in the elastic range.

Therefore, "Hooke's Law" holds for any material, posses homogeneous and isotropic properties, under any types of loadings or load combinations, that behave in a linear elastic manner.

Edit:

The flaw in your thinking is "My guess is that Hooke's law is defined for an infinitesimal cubic element....". In fact, regardless of "size", a material/element exhibits linear stress-strain behavior (linear proportionality of stress and deformation) upon any type of loadings with the stressed plane remains plane, and upon unloading, it returns back to its original shape, is said it is a linear elastic material the Hooke's Law defined for.

ADD (11/2) - Influence of Staged Loadings with Consideration of Stiffness Variations (For Discussion Only)

Answer 3

Hook's law is a first-principled behavior that models the elastic force-distance relationship for axial stretching or compressing of two coupled objects. It is one of the easiest models to use for the behavior of chemical bonds between two atoms or two molecules. It is the common standard to model the behavior of springs. Hook's law can also be extended to the rotating and bending modes of atomic/molecular bonds through suitable translations of coordinate systems or suitable re-definitions of the so-called Hook's law constant.

In reality, chemical bonds between atoms and molecules follow Hook's law only over small perturbations about the equilibrium separation. The more significant deviation from Hook's law generally occurs as a bond is stretched rather than compressed. The extent of the deviation that a chemical bond has from a model parabolic potential well $U = (1/2)k \Delta^2 x$ is associated with the magnitude of the thermal expansion coefficient for the real chemical bond. Or, inversely stated, a chemical bond that followed Hook's law identically until it breaks would have no thermal expansion coefficient.

Hook's law can be extended to macroscopic materials. The required assumption is that force is distributed isotropically in the material. We translate the relationship for transverse force to transverse strain as below where $F$ is force on a bond (N), $k$ is the Hook's law constant (N/m), $\Delta x$ is the deformation (m), $A_o$ is the initial cross-sectional area of the material normal to the applied force (m$^2$), $L_o$ is the initial length of the material (m), $\sigma$ is the normal stress (N/m$^2$ = Pa), $\epsilon$ is the normal strain (m/m), and $E$ is the Young's modulus (Pa).

$$ F = k \Delta x $$

$$\frac{F}{A_o} = \frac{k L_o}{A_o}\ \frac{\Delta x}{L_o} $$

$$ \sigma = E\ \epsilon $$

In summary, when you apply Hook's law to model the force-distance behavior of a bulk material, you are assuming

• the deformation is small (otherwise Hook's law fails to model the true potential of the chemical bond)
• the material is isotropic (otherwise the contributions of the bonds depend on the direction that you apply the force)

An additional concern arises to stay in the small deformation limit. Otherwise, the cross-sectional area $A_o$ is affected (through the Poisson's ratio). The distinction is realized through designations of engineering versus true stress.