High pass filter and differential equation relationship

Question

Consider the problem stated as follows:

A signal y passes through a high pass filter $\frac{s}{s + ω }$. A high pass filter with cutoff frequency ω isolates the variations of this optimized variable from its average value. The state that represents the high pass filter is denoted by η. In the literature, the equation is represented as: $\frac{d η}{d t } = - ω η + ω y$.

My question is, which principle did they use to arrive at that equation. I know that the inverse Laplace transform of $\frac{s}{s + ω }$. will result in a differential equation, as it is being multiplied by s. However, I don’t know how to compute $\frac{s}{s + ω } * y$.

I have attached a screenshot of the control diag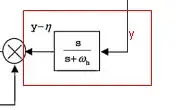ram. I will really appreciate it if someone can please explain this concept to me.

Answer 1

It can be noted that the high-pass filter can also be written as

$$ \frac{s}{s + \omega} = 1 - \frac{\omega}{s + \omega}, $$

such that

$$ \frac{s}{s + \omega} Y(s) = Y(s) - \underbrace{\frac{\omega}{s + \omega} Y(s)}_{\mathcal{L}\{\eta(t)\}(s)}, $$

with $Y(s) = \mathcal{L}\{y(t)\}(s)$ denoting the Laplace transform of $y(t)$.

In order to show that the second term indeed matches $\mathcal{L}\{\eta(t)\}(s)$ one can use that multiplying by $s$ in the $s$-domain is equivalent to taking the derivative with respect to time in the time-domain. Therefore, the following equations are all equivalent

\begin{align} \mathcal{L}\{\eta(t)\}(s) &= \frac{\omega}{s + \omega} \mathcal{L}\{y(t)\}(s), \\ (s + \omega)\,\mathcal{L}\{\eta(t)\}(s) &= \omega\,\mathcal{L}\{y(t)\}(s), \\ \frac{d\,\eta(t)}{dt} + \omega\,\eta(t) &= \omega\,y(t), \\ \frac{d\,\eta(t)}{dt} &= \omega\,(y(t) - \eta(t)). \end{align}

---

One could also try to calculate $\frac{s}{s + \omega} Y(s)$ directly by first differentiating $y(t)$ with respect to time and then passing it through a low-pass filter. However, in general one can not calculate the derivative of every input $y(t)$. Therefore, splitting the high-pass filter into a direct feedthrough minus a low-pass filter makes for a more robust of a calculating the high-pass filter output.

Answer 2

You can show it with Laplace transform. Let's say Y = ℒ[y], H = ℒ[η], and ω_p is the filter pole. (Let's not simply call it ω -- when omega is used as a parameter rather than a variable, a subscript should be added for clarity)

---

dη / dt = ω_p (y - η)

... transform ...

s * H = ω_p ( Y - H )

s * H / ω_p = Y - H

Y = H ( 1 + s/ω_p )

H/Y = 1 / ( 1 + s/ω_p )

which happens to be (surprise!) the transfer function of a one-pole LPF with pole at ω_p.

Thus H and η are the output of an LPF

And so finally, (Y-H), in frequency domain, is (input - LPF), which is HPF here

---

I.e., the transfer functions for LPF = ω_p / ( s + ω_p ), and HPF = s / ( s + ω_p) add up to one.