2

I made a forward fd-discretization of the Cauchy-Riemann PDEs but I am struggling to implement this in python.

I have a quadratic mesh with heighτ = $2*\pi$. The dirichlet boundary conditions are at $u(x,0) = f(x) = \cos(x)$ and $v(x,0) = g(x) = sin(x)$. And I have periodic boundary conditions: $u(2\pi,y) = u(0,y)$ and $v(2\pi,y) = v(0,y)$.

fd-discretization

My code:

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

#meshsize

N=100

U = np.zeros([N,N])

V = np.zeros([N,N])

# dirichlet bc

x = np.linspace(0,2*np.pi,N)



for n in range(0,N):

    V[N-1,n] = np.cos(x[n])

    U[N-1,n] = np.sin(x[n])



# recursion

for i in range(1,N-1):

    for j in range(0,N-1):

        U[i,j] = U[i,j+1] - V[i+1,j] + V[i,j]

        V[i,j] = U[i+1,j] - U[i,j] + V[i,j+1]

        #periodic bc

        dx1 = x[j] - x[i]

        dx = np.mod(dx1, xSize * 0.5)

        V[i-1, 0] = dx

        U[i-1, 0] = dx

        V[i-1, N-1] = dx

        U[i-1, N-1] = dx


# coordinates

x = range(N)

y = range(N)

x, y = np.meshgrid(x, y)



# for interactive plot

%matplotlib notebook



# create plot

fig = plt.figure()

ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(x, y, U, rstride=1, cstride=1, cmap='viridis', edgecolor='none')

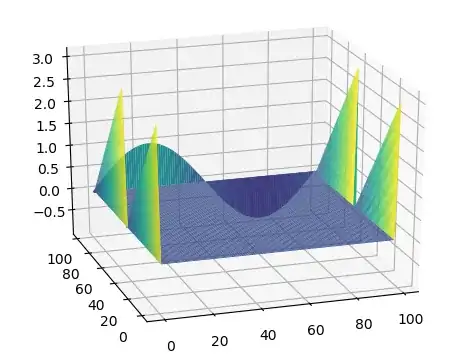
plot of V

I expect the plot to look like the complex e-function $u (x, y) + i\;v(x, y) = exp (ix − y)$ but when I plot U or V there is only the integral of sinus or cosine respectively plotted. I am not sure if my nested for loop does what I want or if I have a lack of understanding how to plot this right. Does anyone have an idea how to solve this?

Rico227
  • 21
  • 3

1 Answers1

0

I can't be to sure, but it looks like there might be going something wrong in these 2 lines:

U[i,j] = U[i,j+1] - V[i+1,j] + V[i,j]

V[i,j] = U[i+1,j] - U[i,j] + V[i,j+1]

See, to compute U[i,j], you need the value of V[i,j], but that is computed in the next line. While that can be solved by substituting the definition in V[i,j] into the equation of U[i,j], there is still another problem. The values of all the forward indexes are computed in an iteration later. To solve that, you either could run the for loop backwards, or perform a backwards discretization.

Petrus1904
  • 1,079
  • 5
  • 5